На этом шаге мы приведем основные термины, которые будут использоваться при изучении бинарных деревьев.

Древовидные структуры получили широкое распространение при решении различных задач, связанных не только с генеалогией. Однако терминология, принятая при описании генеалогических деревьев, сохраняется и при решении другого рода задач. В дальнейшем древовидные структуры мы будем называть просто деревьями.

Определение 1 [1] (неформальное)

Определим дерево как конечное множество T, состоящее из одного или более элементов (называемых вершинами или узлами), таких, что

имеется одна специально выделенная вершина, называемая корнем дерева;
остальные вершины (исключая корень) содержатся в m попарно непересекающихся множествах T1,T2,...,Tm, каждое из которых, в свою очередь, является деревом.

Деревья T1,T2,...Tm называются поддеревьями данного дерева.

Упорядоченным деревом мы будем называть такое дерево, в котором важен порядок следования поддеревьев T1,T2,...Tm.

Дуга - это ориентированная связь между двумя вершинами дерева, поэтому, например, корень можно определить как такую вершину дерева, в который не входит ни одной дуги, поэтому часто говорят, что корень - это "исходная" вершина дерева, через которую доступны остальные его вершины.

Ребро - это неориентированная связь между двумя вершинами дерева. Ясно, что ребро можно превратить в дугу, если задать на нем ориентацию (направление), а любое дерево можно превратить в ориентированное дерево, если задать ориентацию ребер.

Количество поддеревьев некоторой вершины называется степенью этой вершины. Деревья, имеющие степень больше 2, называются сильно ветвящимися деревьями.

Вершина с нулевой степенью называется листом, иначе - она называется внутренней вершиной (внутренним узлом).

Число листьев дерева называется весом дерева.

Символы A,B,C,..., которые служат для обозначения вершин, называются метками вершин.

Приведенное неформальное определение является рекурсивным (мы определили дерево в терминах деревьев). Ниже мы дадим формальное нерекурсивное определение дерева, но рекурсивное определение кажется более подходящим, так как рекурсивность является естественной характеристикой структур типа дерево.

Для удобства дальнейших рассмотрений договоримся о графическом способе изображения деревьев. Корень будем располагать выше поддеревьев (ясно, что корень при изображении будет располагаться выше всех остальных вершин дерева). Вершины дерева будем изображать точками на плоскости, а корень дерева связывать дугами (ребрами) с корнями деревьев T1,T2,...Tm. Взгляните на рисунок и на комментарии, приведенные ниже его:

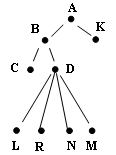
Рис.1. Иллюстрация основных понятий

Символы A, B, C, D, K, L, M, N, R - метки вершин, вершина А - корень, вершины C, L, R, M, N, K - листья, вес дерева равен 6 (количество листьев - 6), вершина В имеет степень 2, вершина D имеет степень 4.

Определение 2 (неформальное)

Вершина Y, которая находится непосредственно под узлом X, называется (непосредственным) потомком (сыном) X, вершина X в данном случае называется (непосредственным) предком (отцом) Y.

В этом случае, если вершина X находится на уровне i, то говорят, что вершина Y находится на уровне i+1. Мы будем считать, что корень дерева расположен на уровне 0. Максимальный уровень какой-либо вершины дерева называется его глубиной или высотой.

Максимальная степень всех вершин дерева называется степенью дерева.

Теперь, например, ясно, что:

если вершина не имеет потомков, то она является листом;
степень внутренней вершины можно определить как число ее (непосредственных) потомков.

Максимальное число вершин в дереве заданной высоты h достигается в случае, когда все вершины имеют по d поддеревьев, кроме вершин уровня h, не имеющих ни одного. Тогда в дереве степени d нулевой уровень содержит одну вершину (корень), первый уровень содержит d ее потомков, второй уровень содержит d² потомков d узлов уровня 2 и т.д.

Таким образом получаем, что максимальное число вершин для дерева с высотой h и степенью d можно найти по формуле:

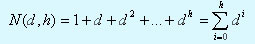
При d=2 мы получаем:

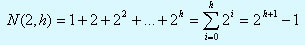
Определение 3 (неформальное)

Количество дуг, которые нужно пройти, чтобы продвинуться от корня к вершине X, называется длиной пути к вершине X. Очевидно, что вершина, расположенная на уровне i, имеет длину пути i.

Ветвью будем называть путь от корня дерева к любому ее листу.

Длина пути дерева определяется как сумма длин путей ко всем его вершинам. Она также называется длиной внутреннего пути дерева.

Длина внутреннего пути может быть определена по следующей рекурсивной формуле:

    Длина внутреннего пути =
          Длина внутреннего пути в левом поддереве +
          Длина внутреннего пути в правом поддереве +
          Количество узлов в дереве - 1.

Для иллюстрации определений приведем рисунок двух деревьев, которые будем предполагать упорядоченными:

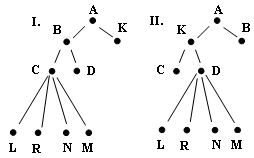
Рис.2. Упорядоченные деревья

В дереве II:

длина пути к вершине L равна 3,
длина пути к вершине К равна 1,
длина внутреннего пути равна 18,
одно из ветвей дерева - AKDL.

Дерево II отличается от дерева I, так как в нем изменен порядок следования поддеревьев с корнями K и B.

Определение 4 [1] (неформальное): Лес - это множество деревьев (обычно упорядоченное), состоящее из некоторого (быть может, равного нулю) числа непересекающихся деревьев. Часто для леса, состоящего из n деревьев пользуются термином "дерево с n-кратным корнем".

Между лесами и деревьями есть лишь небольшое различие; если мы удалим у дерева корень, то получим лес, и наоборот, если к любому лесу добавить всего один узел, то получим дерево.

Приведем пример леса:

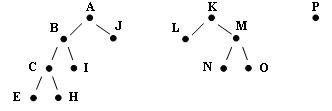
Рис.3. Пример леса

Особое место занимают так называемые бинарные (двоичные) деревья.

Определение 5 [1] (неформальное)

Определим бинарное дерево как конечное множество элементов (называемых вершинами или узлами), которое:

либо пусто,
либо состоит из корня (некоторая выделенная нами вершина), связанного с двумя различными бинарными деревьями, называемыми левым и правым поддеревом корня.

Важно отметить, что бинарное дерево не является частным случаем дерева, определенного выше. Оно представляет собой упорядоченное (см. в определении бинарного дерева слова "...с двумя различными бинарными деревьями...") дерево, у которого в каждую вершину, отличную от корня, входит только одна дуга, а выходит не более двух. При этом для каждой входящей дуги известно, является ли она правой или левой.

Каждая вершина бинарного дерева, отличная от корня, может рассматриваться как корень бинарного поддерева с вершинами, достижимыми из нее.

Изобразим несколько бинарных деревьев:

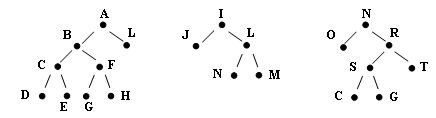
Рис.4. Примеры бинарных деревьев

Определение 6 (неформальное)

Говорят, что два бинарных дерева T и T' подобны, если они имеют одинаковую структуру; это означает, что подобные деревья либо оба пусты, либо оба непусты и их левые и правые поддеревья соответственно подобны.

Попросту говоря, подобие означает, что графические изображения деревьев T и T' имеют одинаковую "конфигурацию".

Говорят, что бинарные деревья T и T' эквивалентны, если они подобны и если, кроме того, соответствующие вершины содержат одинаковую информацию.

Если Info (u) обозначает информацию, содержащуюся в вершине u, то формально деревья эквивалентны тогда и только тогда, когда они:

либо оба пусты,
либо же оба непусты, Info (Корень(T))=Info (Корень(T')) и их левые и правые поддеревья соответственно эквивалентны.

В качестве иллюстрации приведенных определений рассмотрим четыре бинарных дерева:

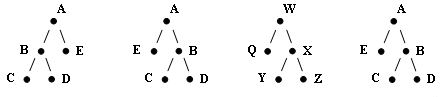
Рис.5. Бинарные деревья

Первые два из них не подобны; второе, третье и четвертое деревья подобны, причем второе и четвертое эквивалентны.

⁽¹⁾Кнут Д. Искусство программирования для ЭВМ. Т.1: Основные алгоритмы. - M.: Мир, 1976. - 736 с.

Со следующего шага мы начнем рассматривать бинарные деревья поиска.

Предыдущий шаг Содержание Следующий шаг