На этом шаге мы рассмотрим алгоритмы построения бинарного дерева.

    Приведем вначале нерекурсивный алгоритм построения дерева поиска. В процессе изложения будет разъяснено, какими свойствами должно обладать бинарное дерево, чтобы быть деревом поиска.

    Обозначим Tree - указатель на корень дерева.

    Tree = NULL; //Построение пустого дерева.

    Обозначим p - вспомогательный указатель на вершину дерева.

1. Пусть ключ первой, поступающей в дерево, вершины равен 100. Создаем первую вершину:

       p = new(node);
       (*p).Key = 100; (*p).Count = 1;
       (*p).Left = NULL; (*p).Right = NULL;
       Tree = p;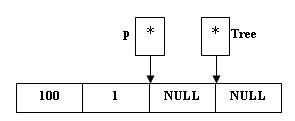
   

   
   Рис.1. Создание первой вершины

2. Пусть ключ второй, поступающей в дерево, вершины равен 50. Выполняем следующие операции:
   • вначале создаем новую вершину:

         p = new(node);
         (*p).Key = 50; (*p).Count = 1;
         (*p).Left = NULL; (*p).Right = NULL;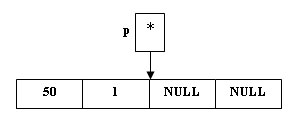
     

     
     Рис.2. Создание новой вершины

   • так как 100>50, то по определению бинарного дерева поиска мы должны сделать вновь поступившую вершину левым сыном корня дерева:

         (*Tree).Left = p;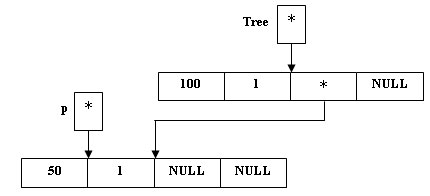
     

     
     Рис.3. Размещение вершины в левом поддереве

3. Пусть ключ третьей вершины, поступающей в дерево, равен 200. Порядок наших действий:
   • создаем новую вершину:

         p = new(node);
         (*p).Key = 200; (*p).Count = 1;
         (*p).Left = NULL; (*p).Right = NULL;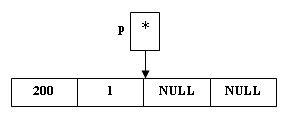
     

     
     Рис.4. Создание новой вершины

   • так как 200>100, то по определению бинарного дерева поиска, мы должны сделать вновь поступившую вершину правым сыном корня дерева:

         (*Tree).Right = p;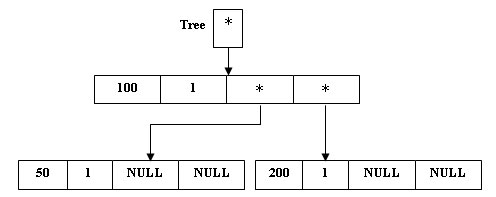
     

     
     Рис.5. Размещение вершины в правом поддереве

    Осталось определить, как же нам действовать в случае поступления, например, в дерево вновь вершины с ключом 100. Оказывается, что поле Count и применяется для учета повторяющихся ключей!

    Точнее, в этом случае выполняется оператор присваивания (*Tree).Count = (*Tree).Count + 1;, результат выполнения которого изобразим на схеме:

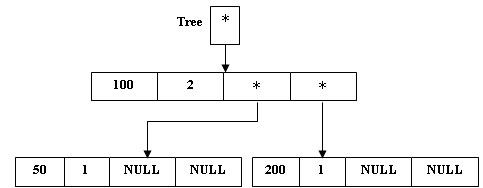
Рис.6. Размещение вершины с ранее встречавшимся ключом

    Таким образом, последовательное поступление вершин с ключами 100, 50, 200, 100 приведет к созданию структуры данных - бинарного дерева поиска.

    Разумеется, написание алгоритма построения дерева поиска с использованием рекурсии или даже просто разбор рекурсивного алгоритма, написанного кем-то другим, далеко не простая задача; она требует большого опыта. Поэтому, мы приводим без комментариев рекурсивную реализацию алгоритма построения дерева:

void BuildTree (node **Tree)
// Построение бинарного дерева. 
// *Tree - указатель на корень дерева.
{
  int el;

  *Tree = NULL; // Построено пустое бинарное дерево.
  cout<<"Вводите ключи вершин дерева...\n";
  cin>>el;
  while (el!=0)
    { Search (el,Tree); cin>>el;}
}

    В функции BuildTree() используется функция поиска вершины с данным ключом x:

void Search (int x, node **p)
// Поиск вершины с ключом x в дереве со вставкой 
// (рекурсивный алгоритм).
// *p - указатель на корень дерева.
{
  if (*p==NULL)
  { // Вершины с ключом x в дереве нет; включить ее.
    *p = new(node);(**p).Key = x; (**p).Count = 1; 
    (**p).Left = (**p).Right = NULL;
  }
  else //Поиск места включения вершины.
    if (x<(**p).Key) //Включение в левое поддерево.
       Search (x,&((**p).Left)); 
    else if (x>(**p).Key) //Включение в правое поддерево.
           Search (x,&((**p).Right)); 
         else (**p).Count = (**p).Count + 1;
}

    Пpогpамма поиска с вставкой по деpеву, котоpая была приведена на этом шаге, отлично подходит для использования в качестве алгоpитма таблиц символов, особенно если желательно выводить символы в алфавитном поpядке.

    На следующем шаге мы проведем анализ приведенного алгоритма поиска с включениями.

Предыдущий шаг Содержание Следующий шаг