На этом шаге мы рассмотрим нерекурсивный алгоритм построения бинарного дерева.

    Рассмотрим нерекурсивный алгоритм построения бинарного дерева поиска, который заключается в циклическом обращении к функции TreeSearch (&Tree,el); где el - значение информационного поля включаемой в дерево Tree вершины. Эта функция осуществляет поиск вершины дерева с информационным полем el и в случае неудачного поиска осуществляет включение вершины с информационным полем el в дерево.

    Опишем лишь начало этого процесса. Н.Вирт [1,с.237] пишет: "Чтобы правильно привязать включаемую компоненту, мы должны иметь ссылку на ее предка и знать, включается она в качестве правого или левого поддерева. Для этого вводятся две переменные p2 и d (для направления)... Используются две ссылки p1 и p2, такие, что в процессе поиска p2 всегда указывает на ... узел дерева, содержащий p1. Чтобы удовлетворить этому условию в начале поиска, вводится вспомогательный фиктивный элемент, на который указывает Tree. Начало действительного дерева поиска обозначается ссылкой (*Tree).Right."

    Формализуем сказанное на языке C++:

1. Создаем "заглавное звено" бинарного дерева:

       Tree = new(node);
       (*Tree).Right = NULL;
       p2 = Tree;
       p1 = (*p2).Right;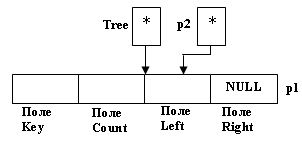
   

   
   Рис.1. Создание "заглавного звена"

2. При поступлении информационного элемента Элем1 первой вершины дерева выполняем следующие команды:

       p1 = new(node);
       (*p1).Key = Элем1; (*p1).Left = (*p1).Right = NULL;
       (*p1).Count = 1;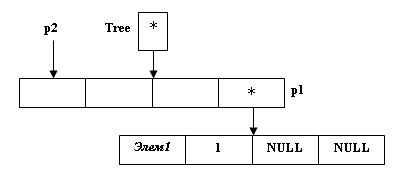 
   

   и получаем:

   
   Рис.2. Размещение первой вершины дерева

3. Далее, в зависимости от поступающего значения информационного поля следующей вершины дерева, структура, содержащая этот элемент, будет "помещаться" либо в правое поддерево (если значение информационного поля больше значения информационного поля корня), либо в левое поддерево (если наоборот), либо будет изменено только содержимое поля Count.

    Запишем алгоритм построения в виде функции на языке C++:

void TreeSearch (node **Tree,int el)
// Поиск вершины с информационным полем el в дереве
// с последующим включением.
// *Tree - указатель на корень дерева.
{
  node *p1;
  node *p2; // Указатель p2 "опережает" указатель p1.
  int d; // Флаг для распознавания поддеревьев.

  p2 = *Tree; p1 = (*p2).Right;
  d = 1; // Флаг правого поддерева.
  while (p1!=NULL && d!=0)
  { p2 = p1; 
    if (el<(*p1).Key) { p1 = (*p1).Left; d = -1; //Флаг левого поддерева. }
    else 
      if (el>(*p1).Key) { p1 = (*p1).Right; d = 1; } 
      else d = 0; }
    if (d==0) (*p1).Count = (*p1).Count + 1;
    else
      { p1 = new(node);
        (*p1).Key = el; (*p1).Left = (*p1).Right = NULL; (*p1).Count = 1; 
        if (d<0) (*p2).Left = p1; else (*p2).Right = p1;}
}

    На следующем шаге мы рассмотрим нерекурсивный алгоритм вывода дерева на экран дисплея.

Предыдущий шаг Содержание Следующий шаг