На этом шаге мы рассмотрим общие операции, выполняемые при включении вершины в сбалансированное дерево.
Рассмотрим теперь, что может произойти при включении в сбалансированное дерево новой вершины. Если у нас есть корень r, левое (L) и правое (R) поддеревья, то необходимо различать три возможных случая. Предположим, что включение в L новой вершины увеличит на 1 его высоту; тогда возможны три случая:
- сначала было hL = hR. После включения L и R станут разной высоты, но критерий сбалансированности не будет нарушен;
- сначала было hL < hR. После включения L и R станут равной высоты, то есть критерий сбалансированности даже улучшится;
- сначала было hL > hR. После включения критерий сбалансированности нарушится и дерево необходимо перестраивать.
Рассмотрим следующее дерево:
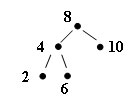
Рис.1. Пример дерева
Вершины с ключами 9 и 11 можно включить в дерево, не нарушив его сбалансированности: дерево с корнем 10 становится односторонним, а дерево с корнем 8 - лучше сбалансированным. Однако включение значений 1, 3, 5 и 7 требует последующей балансировки.
Алгоритм включения и балансировки существенно зависит от того, каким способом хранится информация о сбалансированности дерева. В дальнейшем мы будем хранить в каждой вершине показатель сбалансированности. Таким образом, структура вершины АВЛ-дерева будет следующей:
struct node { int Key; int Count; int bal; // Показатель балансированности вершины. node *Left; node *Right; };
Показатель сбалансированности вершины мы в дальнейшем будем интерпретировать как разность между высотой правого и левого поддерева.
Таким образом, можно сформулировать алгоритм включения вершины в дерево:
- проход по дереву, чтобы убедиться, что включаемого значения в дереве нет;
- включение новой вершины и определение результирующего показателя сбалансированности;
- "отступление" по пути поиска и проверка в каждой вершине показателя сбалансированности. При необходимости - балансировка.
Со следующего шага мы начнем рассматривать алгоритмы балансировки.
