На этом шаге мы рассмотрим реализацию простейших операций над графом, представленным структурой Вирта .
Теперь приведем реализацию на языке C++ простейших операций над графами с использованием структуры Вирта.
Вначале опишем типы данных:
typedef struct L *Lref; //Тип: указатель на заголовочный узел. typedef struct T *Tref; //Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в //списке заголовочных узлов. } Leader; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; } Trailer;
1. Поиск в структуре Вирта заголовочного узла с заданным значением поля Key и добавление его в список заголовочных узлов в случае отсутствия.
Lref SearchGraph (int w, Lref Head, Lref *Tail) //Функция возвращает указатель на заголовочный узел //с ключом w. Если заголовочный узел отсутствует, //то он добавляется в список. Head - указатель на //структуру Вирта. { Lref h; h = Head; (**Tail).Key = w; while ((*h).Key!=w) h = (*h).Next; if (h==*Tail) {//В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. *Tail = new (Leader); (*h).Count = 0; (*h).Trail = NULL; (*h).Next = *Tail;} return h; }
2. Построение структуры Вирта, соответствующей данному ориентированному графу. Перед самым первым обращением к функции создания графа MakeGraph () инициализируем список заголовочных узлов:
Head = new (Leader); Tail = Head;.
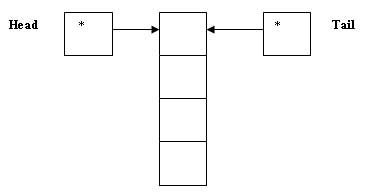
Рис.1. Результат инициализации
Добавление к графу новых вершин и инцидентных им ребер осуществляется обращением к функции MakeGraph().
void MakeGraph (Lref *Head, Lref *Tail) //Функция возвращает указатель *Head на структуру // Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout>>"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? p = SearchGraph (x,*Head,Tail); q = SearchGraph (y,*Head,Tail); r = (*p).Trail; Res = FALSE; while ((r!=NULL) && (!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга не существует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<< "Вводите начальную вершину дуги: "; cin>>x; } }
3. Вывод структуры Вирта, соответствующей ориентированному графу.
void PrintGraph (Lref Head, Lref Tail) //Вывод структуры Вирта, заданной указателем Head и //соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; // Рабочий указатель. p = Head; while (p!=Tail) { cout<<"("<<(*p).Key; q = (*p).Trail; while (q!=NULL) {cout<<(*(*q).Id).Key; q = (*q).Next;} cout<<")"; p = (*p).Next; cout<<" "; } }
Теперь рассмотрим реализацию унарных операций [1, с.22] на графе.
4. Добавление дуги (x,y) (если ее не было) к структуре Вирта, соответствующей ориентированному графу.
void AddGraph (int x,int y, Lref *Head, Lref *Tail) //Добавление дуги (x,y) (если ее не было!) к структуре //Вирта, соответствующей ориентированному графу *Head. { Lref p,q; //Рабочие указатели. Tref t,r; // Рабочие указатели. Boolean Res; //Флаг наличия в графе данной дуги. p = SearchGraph (x,*Head,Tail); q = SearchGraph (y,*Head,Tail); //Определим, существует ли в графе дуга (x,y)? r = (*p).Trail; Res = FALSE; while ((r!=NULL) && (!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) { //Если дуга не существует, то поместим её в граф. t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } }
5. Удаление дуги между двумя вершинами структуры Вирта, определенной указателем Head. Заметим, что концевые вершины дуги из структуры Вирта (а значит, и из графа) не удаляются.
void DeleteGraph (int x,int y, Lref *Head, Lref *Tail) //Функция возвращает указатель *Head на структуру //Вирта, соответствующую ориентированному графу и //полученную удалением дуги (x,y). { Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. // Определим, существует ли в графе дуга (x,y)? p = Search (x,*Head,*Tail);q = Search (y,*Head,*Tail); if ((p!=NULL) && (q!=NULL)) { // Вершины в графе есть. r = (*p).Trail; Res = FALSE; while ((r!=NULL) && (!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (Res) //Если дуга существует, то удалим её. if (r==(*p).Trail) { (*p).Trail = (*(*p).Trail).Next; delete r; (*q).Count--; } else { t = (*p).Trail; while ((*t).Next!=r) t = (*t).Next; (*t).Next = (*(*t).Next).Next; delete r; (*q).Count--; } } }
Lref Search (int w, Lref Head, Lref Tail) //Функция возвращает указатель на заголовочный узел с //ключом w. Если узел отсутствует, то функция возвращает //NULL. { Lref h; h = Head; (*Tail).Key = w; //Поиск "с барьером". while ((*h).Key!=w) h = (*h).Next; if (h==Tail) //В списке заголовочных узлов нет узла с ключом w. h = NULL; return h; }
6. Удаление вершины графа. Необходимо учесть, что удаление вершины v из графа G приводит к подграфу, содержащему все вершины графа G за исключением v, и все ребра графа G, не инцидентные v.
void DeleteY (int y, Lref Head, Lref Tail) //Функция возвращает указатель *Head на структуру Вирта, //соответствующую графу с удаленной вершиной y. { Lref p,q; //Рабочие указатели. Tref r,s; // Рабочие указатели. int x; // Рабочая переменная. //Удаление всех дуг (x,y), оканчивающихся в вершине y. p = *Head; while (p!=*Tail) { x = (*p).Key; DeleteGraph (x,y,Head,Tail);p = (*p).Next; } //Удаление списка смежности вершины y. p = SearchGraph (y,*Head,Tail); r = (*p).Trail; while (r!=NULL) { s = r; r = (*r).Next; delete s; } //Удаление узла, содержащего вершину y, из //списка заголовочных узлов. q = *Head; if (q==p) { *Head = (**Head).Next; delete q;} else { while ((*q).Next!=p) q = (*q).Next; (*q).Next = (*p).Next; delete p; } }
7. Удаление структуры Вирта, соответствующей графу. Не вызывает трудностей написание фрагмента, осуществляющего эту операцию:
. . . t = Head; while (t!=Tail) { Free2Graph (&(*t).Trail); t = (*t).Next; } Free1Graph (&Head,&Tail); delete Tail; . . .
Здесь мы воспользуемся рекурсивными функциями очистки динамической памяти, занятой линейным списком:
void Free1Graph (Lref *Head, Lref *Tail) //Очистка динамической памяти, занятой линейным списком, //заданным указателем *Head. { if (*Head!=*Tail) { Free1Graph (&(**Head).Next,Tail); delete *Head; *Head = NULL; } }
void Free2Graph (Tref *X) //Очистка динамической памяти, занятой линейным списком, //заданным указателем *X. { if (*X!=NULL) { Free2Graph (&(**X).Next); delete *X; *X = NULL; } }
(1) Свами М., Тхуласираман К. Графы, сети и алгоритмы. - М.: Мир, 1984. - 454 с.
На следующем шаге мы приведем пример программы, в которой реализованы рассмотренные операции над графом, представленным структурой Вирта.
