На этом шаге мы рассмотрим общие принципы организации топологической сортировки.

Определение [1, с.324].

Множество M называется частично упорядоченным, если над его элементами определено отношение, которое мы назовем "x предшествует y" и обозначим x<<y, удовлетворяющее следующим свойствам для любых элементов x, y и z из M:

не x<<x (антирефлексивность),
если x<<y, то не y<<x (антисимметричность),
если x<<y и y<<z, то x<<z (транзитивность).

Мы будем предполагать, что M - конечное множество.

Частичное упорядочение на конечном множестве всегда можно проиллюстрировать с помощью диаграммы некоторого графа, в которой элементы представляются вершинами графа, а отношения представляются дугами между этими вершинами; x<<y означает, что от вершины, помеченной x, к вершине y существует путь, идущий вдоль дуг в соответствии с их направлением. Свойство частичного упорядочения означает, что в диаграмме графа нет замкнутых контуров.

Проблема топологической сортировки состоит в том, чтобы "перевести частичное упорядочение в линейное упорядочение", т.е. расположить элементы в такую последовательность a₁,a₂, ..., a_n, что если a_j<<a_k, то j<k [1, с.325]. Существование такого расположения не является непосредственно очевидным, однако оно заведомо невозможно, если имеется хотя бы один контур.

Как найти одно из возможных линейных упорядочений? Рецепт достаточно прост. Мы начинаем с того, что выбираем какой-либо элемент, которому не предшествует никакой другой (хотя бы один такой элемент существует, иначе имелся бы цикл). Этот элемент помещается в начало списка и исключается из множества M. Оставшееся множество по-прежнему частично упорядочено; таким образом, можно вновь применить тот же самый алгоритм, пока множество не станет пустым. Этот алгоритм оказался бы непригодным в единственном случае, когда образовалось бы непустое частично упорядоченное множество, в котором каждому элементу предшествует другой.

Для того, чтобы подробнее сформулировать этот алгоритм, нужно описать структуры данных, а также выбрать представление M и отношения порядка. Это представление зависит от выполняемых действий, особенно от операции выбора элемента без предшественников. Поэтому каждый элемент удобно представить тремя характеристиками:

ключом,
множеством следующих за ним элементов ("последователей") и
счетчиком предшествующих элементов ("предшественников").

Поскольку n - число элементов в M не задано априори, то это множество удобно организовать в виде линейного однонаправленного списка. Следовательно, каждый узел содержит еще поле, связывающее его со следующим узлом списка.

Мы будем считать, что ключи - это целые числа (необязательно последовательные от 1 до n). Аналогично множество последователей каждого элемента можно представить в виде линейного однонаправленного списка. Каждый узел списка последователей неким образом идентифицирован и связан со следующим узлом этого списка.

Если мы назовем узлы главного списка, в котором каждый элемент из M содержится ровно один раз, ведущими (Leaders), а узлы списка последователей ведомыми (Trailers), то мы получим такие описания типов данных [2]:

struct  Leader 
{
    int Key;
    int Count;
    Trailer* Trail;
    Leader* Next;
};

struct Trailer
{
    Leader* Id;
    Trailer* Next;
};

Теперь легко видеть, что описанная структура является структурой Вирта некоторого ориентированного графа.

Первая часть программы топологической сортировки должна преобразовать входные данные в структуру списка. Это производится последовательным чтением пар ключей x и y (x<<y). Мы предполагаем, что последовательность входных пар ключей заканчивается дополнительным нулем.

Обозначим ссылки на их представления в списке ведущих через p и q. Эти записи ищутся в списке и, если их там нет, добавляются к нему. Эту задачу выполняет функция L ("Located"). Затем к списку ведомых для элемента x добавляется новый узел, идентифицированный как y, счетчик предшественников для y увеличивается на 1. Такой алгоритм соответствует фазе ввода.

   //Фаза ввода.
   cout << "Задайте отношение частичного поpядка...\n";
   cout << "Элемент "; 
   cin >> x; 
   cout << " пpедшествует элементу ";
   while  (x!=0)
    {
         cin >> y;
         p = L (x); 
         q = L (y);
         t = new (Trailer); t->Id = q; t->Next = p->Trail;
         p->Trail = t; q->Count += 1;
         cout << "Элемент "; 
         cin >> x;
         cout << " пpедшествует элементу ";
    }

В этом фрагменте программы есть обращения к функции L(w), возвращающей ссылку на компоненту списка с ключом w.

На рисунке показана структура, сформированная при обработке входных данных вида: 1<<4, 1<<2, 4<<8, 5<<8, 2<<8 с помощью этого алгоритма:

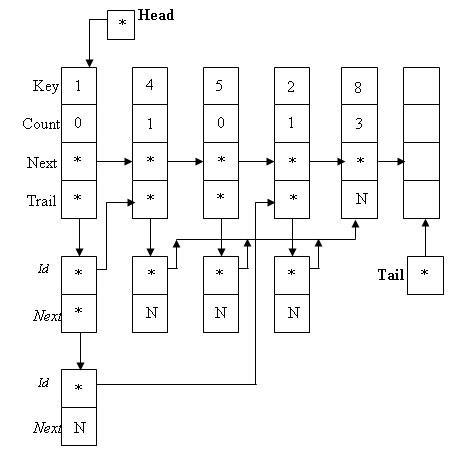
Рис.1. Структура Вирта

После того, как на фазе ввода построена некоторая структура данных, можно провести саму топологическую сортировку, описанную выше. Но поскольку она состоит в последовательном выборе элемента с нулевым счетчиком предшественников, видимо, разумно вначале собрать все такие элементы в некоторый новый список. Поскольку мы знаем, что исходный список ведущих впоследствии не понадобится, то же самое поле Next можно использовать повторно для помещения в список ведущих, не имеющих предшественников. Такая замена одного списка на другой часто встречается при работе со списками.

Это подробно описано в следующем программном фрагменте:

   //Поиск ведущих с нулевым количеством предшественников.
   p = Head; Head = NULL;
   while  (p!=Tail)
    {
      q = p; p = p->Next;
      if (q->Count==0)
        { q->Next = Head; Head = q; }
     }

Для удобства новая цепочка строится в обратном порядке.

Для нашего примера мы увидим, что список ведущих заменяется на список вида:

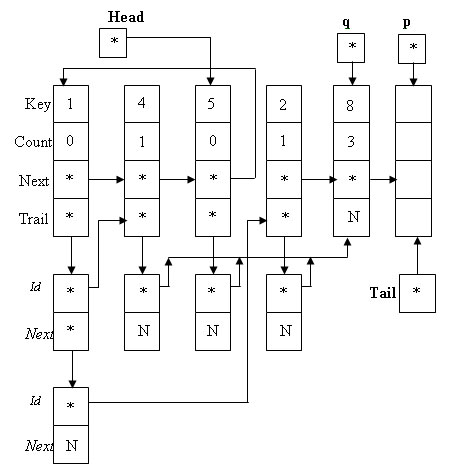
Рис.2. Результат преобразования

После всех этих подготовительных действий, направленных на то, чтобы выработать подходящее представление частично упорядоченного множества M, мы можем, наконец, перейти к собственно топологической сортировке, т.е. формированию выходной последовательности.

Это можно описать следующим образом:

   //Фаза вывода.
   cout << "Результат...\n";
   q = Head;
   while  (q!=NULL)
      {
         //Вывести элемент, а затем исключить его.
         cout << q->Key << " "; z -= 1; t = q->Trail; q = q->Next;
         while  (t!=NULL)
            {
               // Уменьшить счетчик предшественников у всех его  
               // последователей в списке ведомых t; если какой- 
               // либо счетчик стал равен 0, то добавить этот    
               // элемент к списку ведущих q;                    
               // p - вспомогательная переменная, указывающая на 
               // ведущий узел, счетчик которого нужно уменьшить 
               // и проверить на равенство нулю.                  
               p = t->Id; p->Count -= 1;
               if  (p->Count==0) //Включение *p в список ведущих.
                  {  p->Next = q; q = p; }
               t = t->Next;
            }
      }

На этом разработка программы топологической сортировки завершается. Обратите внимание, что был введен счетчик z для подсчета ведущих узлов, сформированных на фазе ввода. Этот счетчик уменьшается каждый раз, когда ведущий узел выводится на фазе вывода. Поэтому он должен вновь стать равным нулю в конце работы программы. Если это не так, то в структуре остались элементы и среди них нет таких, у которых отсутствуют предшественники. Очевидно, что в этом случае множество M не является частично упорядоченным.

Приведенная выше программа фазы вывода служит примером работы со списком, который "пульсирует", т.е. элементы которого добавляются и удаляются в непредсказуемом порядке. Следовательно, это пример процесса, полностью использующего гибкость, которую обеспечивает связанный список.

⁽¹⁾ Кнут Д. Искусство программирования для ЭВМ. Т.1: Основные алгоритмы. - M.: Мир, 1976. - 736 с.
⁽²⁾ Вирт H. Алгоритмы + структуры данных = программы. - М.: Мир, 1985. - 406 с.

Со следующего шага мы начнем приводить примеры программ с использованием топологической сортировки.

Предыдущий шаг Содержание Следующий шаг