На этом шаге мы рассмотрим алгоритм Уоршалла.

    Метод определения матрицы достижимости P графа сначала путем вычисления A, A², ..., Aⁿ, а затем B_n является очень громоздким.

    Опишем более эффективный метод, основанный на аналогичных идеях. Заметим, что нас не интересует число путей любой конкретной длины из вершины v_i в вершину v_j. Эта информация, получаемая в процессе вычисления степеней A, далее игнорируется. Для того, чтобы сократить объем вычислений, можно отказаться от получения указанной информации и использовать в вычислениях просто реализуемые булевские матричные операции, которые мы определим согласно [1, с.440].

    Обозначим булевскую сумму C двух матриц A и B размера n*n как 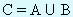, а булевское произведение D - .

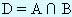    Элементы матриц C и D задаются соотношениями

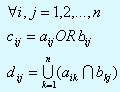
    Заметим, что элемент d_ij легко получается путем просмотра i-й строки матрицы A слева направо и одновременно j-го столбца матрицы B сверху вниз. Если k-й элемент в строке матрицы A и k-й элемент в столбце матрицы B равны 1 для какого-нибудь k, то d_ij=1. В противном случае d_ij=0.

    Булевы матрицы более экономичны в вычислительном отношении, чем целочисленные. Действительно, запоминание булевой матрицы требует меньшего объема оперативной памяти ЭВМ по сравнению с целочисленной матрицей той же размерности. Кроме того, выполнение на компьютере логических операций над булевыми матрицами требует меньшего объема вычислений, чем над целочисленными матрицами тех же размерностей.

    Матрица смежностей, так же как и путевая матрица, является булевской матрицей. Заметим, что .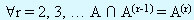

    Единственная разница между A² и A⁽²⁾ заключается в том, что A⁽²⁾ является булевской матрицей и элемент на пересечении i-й строки и j-го столбца A⁽²⁾ равен 1 в том случае, когда существует по крайней мере один путь длины 2 из v_i в v_j. Аналогичное положение имеет место для A³ и A⁽³⁾ и в общем случае для A^r и A^(r) при любом целом положительном r. Из этих рассуждений ясно, что матрица достижимости P задается выражением

    Например, если

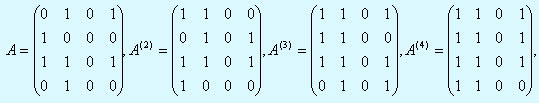
то

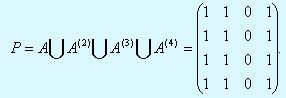
    Данный метод получения матрицы достижимости ориентированного графа называется алгоритмом Уоршалла (Warshall S.A. A Theorem on Boolean Matrices. - J.ACM, 1962, 9, pp.11-12). Он может быть легко реализован на языке C++.

#include <iostream.h>
#define MaxNodes 4

class Warshall
{
  private:
    unsigned Adj[MaxNodes][MaxNodes];  //Матрица смежностей.
    unsigned Path[MaxNodes][MaxNodes]; //Матрица достижимости.
  public:
    void Vvod();
    void TransClose();
    void Vyvod();
};

void Warshall::Vvod()
{
  //Ввод матрицы смежностей заданного графа.
  cout <<"Вводите элементы матрицы смежностей по строкам:\n";
  for (int i=0;i<MaxNodes;i++)
    for (int j=0;j<MaxNodes;j++)
     {
       cout <<"Введите Adj["<< (i+1) << "]["<< (j+1) << "]: ";
       cin >> Adj[i][j];
     }
}

void Warshall::TransClose()
//Вычисление матрицы достижимости.
{
  //Инициализация матрицы Path матрицей смежностей Adj.
  for (int i=0;i<MaxNodes;i++)
    for (int j=0;j<MaxNodes;j++)
      Path[i][j] = Adj[i][j];
  //Нахождение следующих значений матрицы Path.
  for (int k=0;k<MaxNodes;k++)
    for (i=0;i<MaxNodes;i++)
      if (Path[i][k]==1) 
         for (int j=0;j<MaxNodes;j++)
               Path[i][j] = (Path[i][j] || Path[k][j]);
}

void Warshall::Vyvod()
//Вывод матрицы достижимости.
{
  cout << "Матрица достижимости:\n";
  for (int i=0;i<MaxNodes;i++)
  {
    for (int j=0;j<MaxNodes;j++)
      cout << Path[i][j] << " ";
    cout << endl;
  }
}

void main()
{
  Warshall A;
  A.Vvod();
  A.TransClose();
  A.Vyvod();
}

    Заметим, что описанный алгоритм обрабатывает матрицу Adj по столбцам. Уоррен [3, с.320] предложил изящный двухпроходной строкоориентированный алгоритм. В этом алгоритме при обработке вершины, например i, в первом проходе обрабатываются только ребра, связанные с вершинами, меньшими i, а во втором проходе - только ребра, связанные с вершинами, большими i. Другими словами, алгоритм преобразует матрицу смежности Adj графа G в матрицу достижимости, обрабатывая в первом проходе только элементы матрицы, расположенные ниже ее главной диагонали, а во втором проходе - только элементы матрицы, расположенные выше ее главной диагонали. Таким образом, при каждом проходе обрабатывается не более n*(n-1)/2 ребер.

#include <iostream.h>
#define MaxNodes 4

class Warren
{
  private:
    unsigned Adj[MaxNodes][MaxNodes];  //Матрица смежностей.
    unsigned Path[MaxNodes][MaxNodes]; //Матрица достижимости.
  public:
    void Vvod();
    void TransClose();
    void Vyvod();
};

void Warren::Vvod()
{
  //Ввод матрицы смежностей заданного графа.
  cout <<"Вводите элементы матрицы смежностей по строкам:\n";
  for (int i=0;i<MaxNodes;i++)
    for (int j=0;j<MaxNodes;j++)
     {
       cout <<"Введите Adj["<< (i+1) << "]["<< (j+1) << "]: ";
       cin >> Adj[i][j];
     }
}

void Warren::TransClose()
//Вычисление матрицы достижимости.
{
  //Инициализация матрицы Path матрицей смежностей Adj.
  for (int i=0;i<MaxNodes;i++)
    for (int j=0;j<MaxNodes;j++)
      Path[i][j] = Adj[i][j];
  //Нахождение следующих значений матрицы Path.
  for (i=1;i<MaxNodes;i++)
    for (int j=0;j<i;j++)
      if (Path[i][j]==1) 
         for (int k=0;k<MaxNodes;k++)
               Path[i][k] = (Path[i][k] || Path[j][k]);
  for (i=0;i<MaxNodes-1;i++)
    for (int j=i+1;j<MaxNodes;j++)
      if (Path[i][j]==1) 
         for (int k=0;k<MaxNodes;k++)
               Path[i][k] = (Path[i][k] || Path[j][k]);
}

void Warren::Vyvod()
//Вывод матрицы достижимости.
{
  cout << "Матрица достижимости:\n";
  for (int i=0;i<MaxNodes;i++)
  {
    for (int j=0;j<MaxNodes;j++)
      cout << Path[i][j] << " ";
    cout << endl;
  }
}

void main()
{
  Warren A;
  A.Vvod();
  A.TransClose();
  A.Vyvod();
}

    На следующем шаге мы рассмотрим применение алгоритма Уоршалла.

Предыдущий шаг Содержание Следующий шаг