На этом шаге мы рассмотрим особенности заполнения полигонов.

Контур полигона определяется вершинами, которые соединены отрезками прямых (рисунок 1). Это - векторная форма задания фигуры.

Рис.1. Пример полигона

Рассмотрим один из наиболее популярных алгоритмов заполнения полигона. Его основная идея - закрашивание фигуры отрезками прямых линий. Наиболее удобно использовать горизонтали. Алгоритм представляет собою цикл вдоль оси у, в ходе этого цикла выполняется поиск точек сечения линии контура с соответствующими горизонталями. Этот алгоритм получил название XY [1]:

 1. Найти min{у_i} и max{у_i} среди всех вершин P_i.
 2. Выполнить цикл по у от у = min до у = max.
 {
   3. Нахождение точек пересечения всех отрезков контура
    с горизонталью у. Координаты x_j точек сечения записать в массив.
   4. Сортировка массива {x_j} по возрастанию х. 
   5. Вывод горизонтальных отрезков с координатами
      (x₀, у) - (x₁, у)
      (х₂, у) - (х₃, у)
      (х_2k, у) - (x_2k+1, у)
     Каждый отрезок выводится цветом заполнения
 }

В этом алгоритме использовано свойство топологии контура фигуры. Оно состоит в том, что любая прямая линия пересекает любой замкнутый контур четное количество раз (рисунок 2).

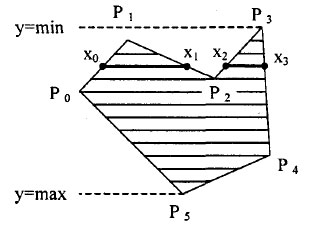
Рис.2. Заполнение полигона

Для выпуклых фигур точек пересечения с любой прямой всегда две. Таким образом, на шаге 3 этого алгоритма в массив {x_j} всегда должно записываться парное число точек сечения.

При нахождении точек пересечения горизонтали с контуром необходимо принимать во внимание особые точки. Если горизонталь имеет координату (у), совпадающую с у_i, вершины P_i, тогда надлежит анализировать то, как горизонталь проходит через вершину. Если горизонталь при этом пересекает контур, как, например, в вершинах Р₀ или Р₄, то в массив записывается одна точка сечения. Если горизонталь касается вершины контура (в этом случае вершина соответствует локальному минимуму или максимуму как, например, в вершинах Р₁, Р₂, Р₃ или Р₅), тогда координата точки касания или не записывается, или записывается в массив два раза. Это условие четности количества точек пересечения, хранящихся в массиве {x_j}.

Процедура определения точек пересечения контура с горизонтальной разверткой, учитывая анализ на локальный максимум, может быть достаточно сложной. Это замедляет работу. Радикальным решением для упрощения поиска точек сечения может быть смещение координат вершин контура или горизонталей заполнения таким образом, чтобы ни одна горизонталь не попала в вершину. Смещение можно выполнять различными способами, например, ввести в растр дробные координаты для горизонталей: y_min+ 0.5, y_min+ 1.5, ..., y_max- 0.5.

Но такое упрощение процедуры нахождения точек пересечения приводит к искажению формы полигона.

Для определения координат (х) точек пересечения для каждой горизонтали необходимо перебирать все n отрезков контура. Координата пересечения отрезка p_i- p_k с горизонталью у равна

  х = х_i + (y_k- y) (х_k - х_i) / (у_k- у_i).

Количество тактов работы этого алгоритма:

  N_тактов ≈ (y_max - y_min) N_гор ,

где y_max, y_min - диапазон координат y, N_гор - число тактов, необходимых для одной горизонтали.

Оценим величину N_гор как пропорциональную числу вершин

  N_гор ≈ k * n,

где k - коэффициент пропорциональности, n - число вершин полигона.

Возможны модификации приведенного алгоритма для ускорения его работы. Например, можно принять во внимание то, что каждая горизонталь в большинстве случаев пересекает небольшое количество ребер контура. Поэтому если при поиске точек сечения делать предварительный отбор ребер, которые находятся вокруг каждой горизонтали, то можно добиться уменьшения количества тактов работы с N_гор= k * n до k * n_p, где n_p - число отобранных ребер. Например, разделим диапазон y_min- y_max пополам. Если для диапазона от y_min до y_ср составить список отрезков (или вершин), которые попадают в этот диапазон, то в этот список будет включено приблизительно вдвое меньшее количество, чем для всего диапазона от y_min до y_max. Почему приблизительно - ибо это зависит от формы полигона. Таким образом, при работе алгоритма для каждой горизонтали в диапазоне y_min до у_ср уже нужно не k * n тактов, а ∼ k * n/2. Аналогично для диапазона у_ср- y_max также можно составить список ребер, который также будет почти вдвое меньшим. Если принять, что подсчеты для каждой горизонтали теперь выполняются за вдвое меньшее количество тактов, а именно за (Nгор/2), то общее число тактов:

  N_тактов ≈ (y_max - y_min) N_гор/2 + N_доп ,

где N_доп - количество тактов для создания списка ребер.

Такой способ повышения быстродействия эффективен для большого количества вершин. Контур можно делить не пополам, а на более мелкие части - соответственно повышается скорость.

Приведенные на предыдущих шагах алгоритмы заполнения могут быть использованы не только для рисования фигур. На основе алгоритмов заполнения могут быть разработаны алгоритмы для других целей. Например, для определения площади фигуры, если считать площадь пропорциональной количеству пикселей заполнения. Или, например, алгоритм для поиска объектов по внутренней точке - эта операция часто используется в векторных графических редакторах.

⁽¹⁾Эгрон Ж. Синтез изображений. Базовые алгоритмы. - М.: Радио и связь, 1993. - 316 с.

Со следующего шага мы начнем знакомиться со стилем линии.

Предыдущий шаг Содержание Следующий шаг