На этом шаге мы рассмотрим особенности множеств и мультимножеств.
Множества и мультимножества, как и все стандартизированные классы ассоциативных контейнеров, обычно реализуются в виде сбалансированного бинарного дерева (рисунок 1).
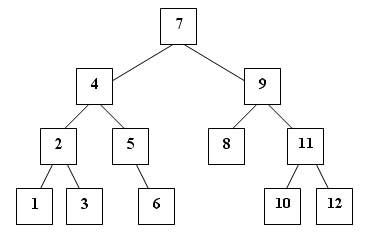
Рис.1. Внутренняя структура множеств и мупьтимножеств
В стандарте такая реализация не указана, но она обусловлена требованиям к сложности операций над множествами и мультимножествами.
Замечание. Точнее говоря, множества и мультимножества обычно реализуются в виде бинарных деревьев. Эти деревья хорошо приспособлены как для изменения количества элементов, так и для поиска. Они гарантируют, что вставка потребует не более двух изменений внутренних ссылок, а самый длинный путь к элементу будет не более чем вдвое длиннее самого короткого.
Главное достоинство автоматической сортировки заключается в том, что бинарное дерево обеспечивает хорошие показатели при поиске элементов с конкретным значением. Функции поиска в них имеют логарифмическую сложность. Например, чтобы найти элемент в множестве или мультимножестве, содержащем 1000 элементов, процедуре поиска по дереву (функции класса) потребуется выполнить в среднем около 1/50 от количества сравнений при линейном поиске (алгоритм). За дополнительной информацией о сложности операций обращайтесь на 42 шаг.
Тем не менее автоматическая сортировка также накладывает важное ограничение на множества и мультимножества: значение элементов нельзя изменять напрямую, потому что это может нарушить правильный порядок их расположения. Следовательно, чтобы изменить значение элемента, необходимо удалить элемент со старым значением и вставить элемент с новым значением. Этот принцип нашел свое отражение в интерфейсе:
- множества и мультимножества не поддерживают прямое обращение к элементам;
- при косвенном обращении через итераторы действует ограничение: с точки зрения итератора значение элемента является константным.
Со следующего шага мы начнем знакомиться с операциями над множествами и мультимножествами.
