На этом шаге мы рассмотрим итераторы произвольного доступа.

    Итераторами произвольного доступа называются двунаправленные итераторы, поддерживающие прямой доступ к элементам. Для этого в них определяются "вычисления с итераторами" (по аналогии с математическими вычислениями с обычными указателями) - вы можете складывать и вычитать смещения, обрабатывать разности и сравнивать итераторы при помощи операторов отношения (таких, как < и >). В таблице 1 перечислены дополнительные операции для итераторов произвольного доступа.

Таблица 1. Дополнительные операции для итераторов произвольного доступа

Выражение	Описание
iter[n]	Обращение к элементу с индексом n
iter+=n	Смещение на n элементов вперед (или назад, если n<0)
iter-=n	Смещение на n элементов назад (или вперед, если n<0)
iter+n	Возвращает итератор для n-го элемента вперед от текущей позиции
n+iter	Возвращает итератор для n-го элемента вперед от текущей позиции
iter-n	Возвращает итератор для n-го элемента назад от текущей позиции
iter1-iter2	Возвращает расстояние между iter1 и iter2
iter1<iter2	Проверяет, что iter1 меньше iter2
iter1>iter2	Проверяет, что iter1 больше iter2
iter1<=iter2	Проверяет, что iter1 предшествует или совпадает с iter2
iter1>=iter2	Проверяет, что iter1 не предшествует iter2

    Итераторы произвольного доступа поддерживаются следующими объектами и типами:

• контейнеры с произвольным доступом (vector, deque);
• строки (string, wstring);
• обычные массивы (указатели).

    Представленная ниже программа демонстрирует особые возможности итераторов произвольного доступа.

//---------------------------------------------------------------------------

#include <vcl.h>
#include <iostream>
#include <iterator>
#include <vector>

#include <conio.h> //необходимо для getch()

#pragma hdrstop

//---------------------------------------------------------------------------

#pragma argsused
using namespace std;


std::string ToRus(const std::string &in)
{
  char *buff = new char [in.length()+1];
  CharToOem(in.c_str(),buff);
  std::string out(buff);
  delete [] buff;
  return out;
}


int main(int argc, char* argv[])
{
  vector<int> coll;

  // Вставка элементов от -3 до 9
  for (int i=-3; i<=9; ++i) {
    coll.push_back (i);
  }

  // Вывод количества элементов как расстояния между
  // начальным и конечным итераторами
  // - ВНИМАНИЕ: применение оператора - для итераторов

  cout << ToRus("число/расстояние: ") << coll.end()-coll.begin() << endl;

  // Вывод всех элементов
  // - ВНИМАНИЕ: применение оператора < вместо оператора !=
  cout << ToRus("Элементы:\n");
  vector<int>::iterator pos;
  for (pos=coll.begin(); pos<coll.end(); ++pos) {
    cout << *pos << ' ';
  }  
  cout << endl;

  // Вывод всех элементов
  // - ВНИМАНИЕ: применение оператора [] вместо оператора *
  cout << ToRus("Элементы:\n");
  for (int i=0; i<coll.size(); ++i) {
    cout << coll.begin()[i] << ' ';
  }
  cout << endl;

  // Вывод каждого второго элемента
  // - ВНИМАНИЕ: применение оператора +=
  cout << ToRus("Вывод каждого второго элемента:\n");
  for (pos = coll.begin(); pos < coll.end()-1; pos += 2) {
    cout << *pos << ' ';
  }
  cout << endl;

  getch();
  return 0;
}

//---------------------------------------------------------------------------

    Результат выполнения программы выглядит так:

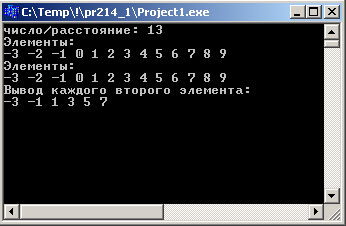
Рис.1. Результат работы приложения

    Этот пример не работает со списками, множествами и отображениями, потому что все операции с пометкой ВНИМАНИЕ: поддерживаются только для итераторов произвольного доступа. В частности, помните, что оператор < может использоваться в критерии завершения цикла только для итераторов произвольного доступа.

    Следующее выражение в последнем цикле требует, чтобы коллекция coll содержала минимум один элемент:

  pos < coll.end()-1

    Если коллекция пуста, то coll.end()-1 будет ссылаться на позицию перед coll.begin(). Сравнение останется работоспособным, но, формально говоря, перемещение итератора в позицию перед началом коллекции приводит к непредсказуемым последствиям. То же самое происходит при выходе за пределы конечного итератора end() при выполнении выражения pos+=2. Таким образом, следующая формулировка последнего цикла очень опасна, потому что при четном количестве элементов в коллекции она приводит к непредсказуемым последствиям (рисунок 2):

  for (pos = coll.begin(); pos < coll.end(); pos += 2) { 
    cout << *pos << ' ';
  }

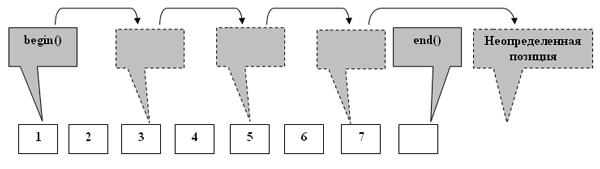
Рис.2. Ошибочная ситуация

    На следующем шаге мы рассмотрим проблему увеличения и уменьшения итераторов в векторах.

Предыдущий шаг Содержание Следующий шаг