На этом шаге мы рассмотрималгоритмы поиска первых n последовательных совпадений.

Для организации такого поиска можно использовать следующие алгоритмы:

  InputIterator
  search_n (InputIterator beg, InputIterator end, Size count, const T& value)
  InputIterator
  search_n (Inputlterator beg, Inputlterator end, 
            Size count, const T& value, BinaryPredicate op)

Первая форма возвращает позицию первого из count последовательных элементов в интервале [beg,end), каждый из которых имеет значение value.

Вторая форма возвращает позицию первого из count последовательных элементов в интервале [beg,end), для которых бинарный предикат op(elem,value) возвращает true.

Если подходящий элемент не найден, обе формы возвращают end.

Предикат ор не должен изменять свое состояние во время вызова, а также передаваемые аргументы.

Сложность линейная (не более numberOfElementsxcount сравнений или вызовов ор соответственно).

Пример поиска трех последовательных элементов со значениями, большими либо равными 3:

//---------------------------------------------------------------------------

#include <vcl.h>
#include <iterator>
#include "algostuff.hpp"

#include <conio.h> //необходимо для getch()

#pragma hdrstop

//---------------------------------------------------------------------------

#pragma argsused
using namespace std;

std::string ToRus(const std::string &in)
{
  char *buff = new char [in.length()+1];
  CharToOem(in.c_str(),buff);
  std::string out(buff);
  delete [] buff;
  return out;
}

int main()
{
 deque<int> coll;

 INSERT_ELEMENTS(coll,1,9);
 cout << ToRus("Исходный дек:\n");
 PRINT_ELEMENTS(coll);

 // Поиск четырех последовательных элементов со значением 3
 deque<int>::iterator pos;
 pos = search_n (coll.begin(), coll.end(),    // Интервал
                 4,                           // Счетчик
                 3);                          // Значение

 // Вывод результата
 if (pos != coll.end()) {
     cout << ToRus("Четыре последовательно идущих элемента со значенеим 3 ")
          << ToRus("начинаются с позиции ") << distance(coll.begin(),pos) +1
          << "." << endl;
   }
 else {
     cout << ToRus("Нет четырех последовательно идущих элементов со значением 3")
          << endl;
   }

 // Поиск четырех последовательных элементов со значением, большим 3
 pos = search_n (coll.begin(), coll.end(),    // Интервал
                 4,                           // Счетчик
                 3,                           // Значение
                 greater<int>());             // Критерий

 // Вывод результата
 if (pos != coll.end()) {
     cout << ToRus("Четыре подряд идущих элемента, значения которых больше 3,\n")
            << ToRus("начинаются с ") << distance(coll.begin(),pos) +1
            << ToRus(" позиции.") << endl;
 }
 else {
     cout << ToRus("Нет четырех последовательно идущих элементов со значением, 
                    большим  3")
          << endl;
 }


  getch();
  return 0;
}

//---------------------------------------------------------------------------

Текст этого примера можно взять здесь.

Результат выполнения программы:

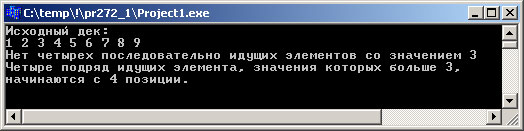
Рис.1. Результат работы приложения

При использовании второй формы алгоритма search_n() возникает весьма неприятная проблема. Рассмотрим второй вызов search_n():

  pos = search_n (coll.begin(),coll.end(), // Интервал
                  4,                       // Счетчик
                  3,	                   // Значение
                  greater<int>0);          // Критерий

Такая семантика поиска элементов, удовлетворяющих заданному критерию, отличается от той, что используется в других компонентах STL. По канонам STL этот вызов должен выглядеть так:

  pos = search_n_if (coll.begin(), coll.end(),          // Интервал
                     4,                                 // Счетчик
                     bind2nd(greater<int>(),3));        // Критерий

Некоторые даже полагают, что версия с четырьмя аргументами более удобна, однако она требует бинарного предиката даже в том случае, когда по логике должно быть достаточно унарного предиката. Например, конструкция с пользовательской унарной предикатной функцией обычно выглядит так:

  bool isPrime (int elem);
  .    .   .   .
  pos = search_n_if (coll.begin(), coll.end(),  // Интервал
                     4,                         // Счетчик
                     isPrime);                  // Критерий

Однако на практике алгоритм требует, чтобы вы использовали бинарный предикат. Из-за этого приходится либо менять сигнатуру функции, либо писать функцию-оболочку:

  bool binaryIsPrime (int eleml. int) { 
    return isPrime(elem1);
  }
  .   .   .   .
  pos = search_n (coll.begin(),coll.end(),   // Интервал
                  4,                         // Счетчик
                  0,                         // Фиктивное значение
                  binaryIsPrime);            // Бинарный критерий

На следующем шаге мы рассмотрим поиск первого подинтервала.

Предыдущий шаг Содержание Следующий шаг