На этом шаге мы рассмотрим алгоритмы, используемые для перестановки элементов.

Для выполнения перестановки элементов существуют следующие алгоритмы:

  bool
  next_permutation (BidirectionalIterator beg, BidirectionalIterator end)
  bool
  prev_permutation (BidirectionalIterator beg, BidirectionalIterator end)

Алгоритм next_permutation() изменяет порядок следования элементов в интервале [beg,end) в соответствии со следующей перестановкой.

Алгоритм prev_permutation() изменяет порядок следования элементов в интервале [beg,end) в соответствии с предыдущей перестановкой.

Оба алгоритма возвращают false, если элементы находятся в "нормальном" (лексикографическом) порядке, то есть упорядочены по возрастанию для next_ permutation() или по убыванию для prev_permutation(). Следовательно, для того чтобы перебрать все перестановки, нужно отсортировать элементы (по возрастанию или убыванию) и организовать цикл, который вызывает алгоритм next_ permutation() или prev_permutation() до тех пор, пока алгоритм возвращает true.

Замечание. Алгоритмы next_permutation() и prev_permutation() также могут использоваться для сортировки элементов в интервале - просто вызывайте их до тех пор, пока возвращаемое значение остается равным true. Впрочем, такой способ сортировки отличается очень плохой эффективностью.

Сложность линейная (не более numberOfElements/2 обменов).

Следующий пример показывает, как при помощи алгоритмов next_permutation() и prev_permutation() генерируются все перестановки элементов:

//---------------------------------------------------------------------------

#include <vcl.h>
#include <iterator>
#include "algostuff.hpp"

#include <conio.h> //необходимо для getch()

#pragma hdrstop

//---------------------------------------------------------------------------

#pragma argsused
using namespace std;

std::string ToRus(const std::string &in)
{
  char *buff = new char [in.length()+1];
  CharToOem(in.c_str(),buff);
  std::string out(buff);
  delete [] buff;
  return out;
}

int main()
{
  vector<int> coll;

  INSERT_ELEMENTS(coll,1,3);
  PRINT_ELEMENTS(coll,"Исходный вектор:\n");

  // Генерировать перестановки элементов до тех пор, пока они
  //   не будут упорядочены
  //   - при этом перебираются все возможные перестановки,
  //   - потому что в исходном состоянии
  //   - элементы упорядочены по возрастанию
  cout << ToRus("Перестановки:\n");
  while (next_permutation(coll.begin(),coll.end())) {
      PRINT_ELEMENTS(coll," ");
  }
  PRINT_ELEMENTS(coll,"Исходная перестановка:\n");

  // Генерировать перестановки элементов до тех пор,
  //   пока элементы не будут упорядочены по убыванию
  //   - это будет следующая перестановка после сортировки
  //   - по возрастанию, поэтому цикл сразу же завершается
  while (prev_permutation(coll.begin(),coll.end())) {
      PRINT_ELEMENTS(coll," ");
  }
  PRINT_ELEMENTS(coll,"Конечная перестановка:\n");

  // Генерировать перестановки элементов до тех пор,
  //   пока элементы не будут упорядочены по убыванию
  //   - при этом перебираются все возможные перестановки,
  //   - потому что в исходном состоянии
  //   - элементы упорядочены по убыванию
  while (prev_permutation(coll.begin(),coll.end())) {
      PRINT_ELEMENTS(coll," ");
  }
    PRINT_ELEMENTS(coll,"Перестановка:\n");


  getch();
  return 0;
}

//---------------------------------------------------------------------------

Текст этого примера можно взять здесь.

Результат выполнения программы выглядит так:

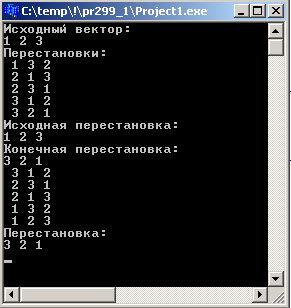
Рис.1. Результат выполнения приложения

На следующем шаге мы рассмотрим перестановку элементов в случайном порядке.

Предыдущий шаг Содержание Следующий шаг