На этом шаге мы рассмотрим пример использования рассмотренных на предыдущем шаге алгоритмов.
Следующая программа демонстрирует использование различных алгоритмов работы с кучей:
//--------------------------------------------------------------------------- #include <vcl.h> #include <iterator> #include "algostuff.hpp" #include <conio.h> //необходимо для getch() #pragma hdrstop //--------------------------------------------------------------------------- #pragma argsused using namespace std; std::string ToRus(const std::string &in) { char *buff = new char [in.length()+1]; CharToOem(in.c_str(),buff); std::string out(buff); delete [] buff; return out; } int main() { vector<int> coll; INSERT_ELEMENTS(coll,3,7); INSERT_ELEMENTS(coll,5,9); INSERT_ELEMENTS(coll,1,4); PRINT_ELEMENTS (coll,"Исходная коллекция:\n"); // Преобразование коллекции в кучу make_heap (coll.begin(), coll.end()); PRINT_ELEMENTS (coll, "После применения make_heap():\n"); // Извлечение следующего элемента из кучи pop_heap (coll.begin(), coll.end()); coll.pop_back(); PRINT_ELEMENTS (coll, "После применения pop_heap():\n"); // Занесение нового элемента в кучу coll.push_back (17); push_heap (coll.begin(), coll.end()); PRINT_ELEMENTS (coll, "После применения push_heap():\n"); // Преобразование кучи в упорядоченную коллекцию // - ВНИМАНИЕ: после вызова интервал перестает быть кучей sort_heap (coll.begin(), coll.end()); PRINT_ELEMENTS (coll, "После применения sort_heap():\n"); getch(); return 0; } //---------------------------------------------------------------------------
Результат выполнения программы выглядит так:
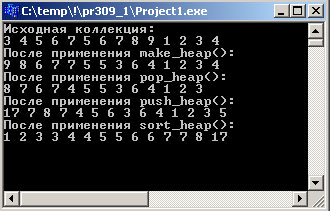
Рис.1. Результат работы приложения
После вызова make_heap() элементы сортируются в виде кучи:
9 8 6 7 7 5 5 3 6 4 1 2 3 4
Если преобразовать эту последовательность в бинарное дерево, вы увидите, что значение каждого узла меньше либо равно значению его родительского узла (рисунок 2).
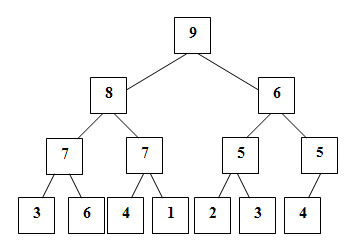
Рис.2. Элементы кучи в виде бинарного дерева
Алгоритмы push_heap() и рор_hеар() изменяют элементы так, что инвариант структуры бинарного дерева (любой узел не больше своего родительского узла) остается неизменным.
Со следующего шага мы начнем рассматривать алгоритмы упорядоченных интервалов.
