На этом шаге мы рассмотрим алгоритмы поиска первой или последней возможной позиции.

Для решения указанных задач можно воспользоваться следующими алгоритмами:

  ForwardIterator
  lower_bound (ForwardIterator beg, ForwardIterator end, 
               const T& value)

  ForwardIterator
  lower_bound (ForwardIterator beg, ForwardIterator end, 
               const T& value, BinaryPredicate op)

  ForwardIterator
  upper_bound (ForwardIterator beg, ForwardIterator end, 
               const T& value)

  ForwardIterator
  upper_bound (ForwardIterator beg, ForwardIterator end, 
               const T& value, BinaryPredicate op)

Алгоритм lower_bound() возвращает позицию первого элемента со значением, большим либо равным value. Результат определяет первую позицию, в которой элемент со значением value вставляется без нарушения упорядоченности интервала [beg,end).

Алгоритм upper_bound() возвращает позицию первого элемента со значением, большим value. Результат определяет первую позицию, в которой элемент со значением value вставляется без нарушения упорядоченности интервала [beg,end).

Если позицию найти не удалось, оба алгоритма возвращают end.

В необязательном параметре ор передается бинарный предикат, определяющий критерий сортировки: op(elem1,elem2).

Перед вызовом интервал должен быть упорядочен по соответствующему критерию сортировки.

Чтобы одновременно получить результаты алгоритмов lower_bound() и upper_bound(), воспользуйтесь алгоритмом equal_range(), который возвращает оба значения.

В ассоциативных контейнерах (множество, мультимножество, отображение и мультиотображение) определены эквивалентные функции, которые работают более эффективно (смотри 198 шаг).

Сложность логарифмическая для итераторов произвольного доступа, линейная в остальных случаях (не более log(numberOfElements)+1 сравнений, но для итераторов, не являющихся итераторами произвольного доступа, выполняется линейное количество операций перебора, вследствие чего сложность оказывается линейной).

Пример использования алгоритмов lower_bound() и upper_bound():

//---------------------------------------------------------------------------

#include <vcl.h>
#include <iterator>
#include "algostuff.hpp"

#include <conio.h> //необходимо для getch()

#pragma hdrstop

//---------------------------------------------------------------------------

#pragma argsused
using namespace std;

std::string ToRus(const std::string &in)
{
  char *buff = new char [in.length()+1];
  CharToOem(in.c_str(),buff);
  std::string out(buff);
  delete [] buff;
  return out;
}

int main()
{
  list<int> coll;

  INSERT_ELEMENTS(coll,1,9);
  INSERT_ELEMENTS(coll,1,9);
  coll.sort ();
  PRINT_ELEMENTS(coll,"Исходная коллекция:\n");

  // Вывод первой и последней позиций, в которых может быть
  // вставлен элемент со значением 5
  list<int>::iterator pos1, pos2;

  pos1 = lower_bound (coll.begin(), coll.end(),
                      5);
  pos2 = upper_bound (coll.begin(), coll.end(),
                      5);
  cout << ToRus("Число 5 может быть вставлено с ")
       << distance(coll.begin(),pos1) + 1
       << ToRus(" по ")
       << distance(coll.begin(),pos2) + 1
       << ToRus("\nпозицию без нарушения упорядоченности.") << endl;

  // Вставка 3 в первой возможной позиции без нарушения упорядоченности
  coll.insert (lower_bound(coll.begin(),coll.end(),
                           3),
               3);

  // Вставка 7 в первой возможной позиции без нарушения упорядоченности
  coll.insert (upper_bound(coll.begin(),coll.end(),
                           7),
               7);

  PRINT_ELEMENTS(coll,"Коллекция после вставки 3 и 7:\n");


  getch();
  return 0;
}

//---------------------------------------------------------------------------

Текст этого примера можно взять здесь.

Программа выводит следующий результат:

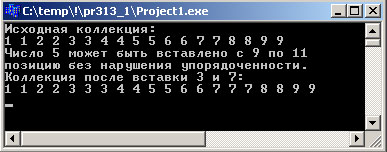
Рис.1. Результат работы приложения

На следующем шаге мы рассмотрим поиск первой и последней возможных позиций.

Предыдущий шаг Содержание Следующий шаг