На этом шаге мы рассмотрим алгоритмы суммирования двух упорядоченных множеств элементов.

    Алгоритмы, представленные в этом и следующих шагах, комбинируют элементы двух интервалов и вычисляют результирующий итератор - сумму, объединение, пересечение и т. д.

Суммирование двух упорядоченных множеств элементов

    Для выполнения данного действия могут использоваться следующие алгоритмы:

  OutputIterator
  merge (InputIterator source1Beg, InputIterator source1End,
         InputIterator source2Beg, InputIterator source2End,
         Outputlterator destBeg)

  OutputIterator
  merge (InputIterator source1Beg, InputIterator source1End.
         InputIterator source2Beg, InputIterator source2End,
         OutputIterator destBeg, BinaryPredicate op)

    Обе формы комбинируют элементы упорядоченных исходных интервалов [source1Beg,source1End) и [source2Beg,source2End) таким образом, что приемный интервал [destBeg,...) содержит все элементы как первого, так и второго интервалов. Например, рассмотрим два интервала:

 1 2 2 4 6 7 7 9 
 2 2 2 3 6 6 8 9

    В результате вызова алгоритма merge() для этих интервалов будет получен следующий интервал:

 1 2 2 2 2 2 3 4 6 6 6 7 7 8 9 9

    В приемном интервале элементы следуют в порядке сортировки.

    Обе формы возвращают позицию за последним скопированным элементом в приемном интервале (то есть позицию первого элемента, который не был переписан).

    В необязательном параметре ор передается бинарный предикат, определяющий критерий сортировки: op(elem1,elem2).

    Алгоритмы не изменяют состояние исходных интервалов.

    Согласно стандарту, оба исходных интервала должны быть упорядочены перед вызовом. Впрочем, в большинстве реализаций алгоритм merge() также комбинирует неупорядоченные исходные интервалы в неупорядоченный приемный интервал. Но чтобы сохранить переносимость программы, вызов merge() следует заменить двукратным вызовом сору().

    Перед вызовом необходимо убедиться в том, что приемный интервал имеет достаточный размер, или использовать итераторы вставки.

    Приемный интервал не должен перекрываться с исходными интервалами.

    Для списков определена аналогичная функция merge(), комбинирующая элементы двух списков (смотри 204 шаг).

    Чтобы элементы, присутствующие в обоих исходных интервалах, включались в приемный интервал только один раз, используйте алгоритм set_union().

    Чтобы в приемный интервал включались только элементы, присутствующие в обоих исходных интервалах, используйте алгоритм set_intersection().

    Сложность линейная (не более numberOfElements1+numberOfElements2-1 сравнений).

    Пример использования алгоритма merge():

//---------------------------------------------------------------------------

#include <vcl.h>
#include <iterator>
#include "algostuff.hpp"

#include <conio.h> //необходимо для getch()

#pragma hdrstop

//---------------------------------------------------------------------------

#pragma argsused
using namespace std;

std::string ToRus(const std::string &in)
{
  char *buff = new char [in.length()+1];
  CharToOem(in.c_str(),buff);
  std::string out(buff);
  delete [] buff;
  return out;
}

int main()
{
  list<int> coll1;
  set<int> coll2;

  // Заполнение обеих коллекций упорядоченными элементами
  INSERT_ELEMENTS(coll1,1,6);
  INSERT_ELEMENTS(coll2,3,8);

  PRINT_ELEMENTS(coll1,"1-я коллекция:\n");
  PRINT_ELEMENTS(coll2,"2-я коллекция:\n");

  // Вывод результата слияния
  cout << ToRus("Результат слияния:\n");
  merge (coll1.begin(), coll1.end(),
         coll2.begin(), coll2.end(),
         ostream_iterator<int>(cout," "));
  cout << endl;


  getch();
  return 0;
}

//---------------------------------------------------------------------------

    Результат выполнения программы выглядит так:

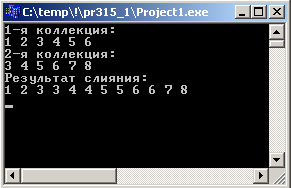
Рис.1. Результат работы приложения

    На следующем шаге мы рассмотрим объединение двух упорядоченных множеств элементов.

Предыдущий шаг Содержание Следующий шаг