На этом шаге мы рассмотрим алгоритмы, используемые для вычисления скалярного произведения двух интервалов.
Для выполнения этой операции можно использовать следующие алгоритмы:
T
inner_product (InputIterator1 beg1, InputIterator1 end1,
InputIterator2 beg2, T initValue)
T
inner_product (InputIterator1 beg1, InputIterator1 end1,
InputIterator2 beg2, T initValue,
BinaryFunc op1, BinaryFunc op2)
Первая форма вычисляет и возвращает скалярное произведение initValue и элементов интервалов [beg,end) и [beg2,...). Для каждого элемента выполняется команда:
initValue = initValue + elem1 * elem2
Вторая форма вычисляет и возвращает накопленный результат вызова ор для initValue и элементов интервала [beg,end), объединенных с элементами [beg2,...). Для каждого элемента выполняется команда:
initValue = op1(initValue,op2(elem1,elem2))
Таким образом, пусть мы имеем следующие значения:
a1 а2 а3 а4... b1 b2 b3 ...
Для этих значений соответственно вычисляются и записываются такие величины:
initValue + (a1 * b1) + (а2 * b2) + (a3 * b3) + ... initValue op1 (al ор2 b1 op1 (а2 ор2 b2) op1 (a3 ор2 b3) op1 ...
Для пустого первого интервала (beg1 == end1) обе формы возвращают initValue.
Перед вызовом необходимо убедиться в том, что интервал [beg2,...) содержит достаточное количество элементов.
Предикаты ор1 и ор2 не должны модифицировать передаваемые аргументы.
Сложность линейная (numberOfElements вызовов операторов + и * или numberOfElements вызовов ор1() и ор2() соответственно).
В следующем примере алгоритм inner_product() используется для вычисления суммы произведений и произведения сумм элементов двух интервалов.
//--------------------------------------------------------------------------- #include <vcl.h> #include <iterator> #include "algostuff.hpp" #include <conio.h> //необходимо для getch() #pragma hdrstop //--------------------------------------------------------------------------- #pragma argsused using namespace std; std::string ToRus(const std::string &in) { char *buff = new char [in.length()+1]; CharToOem(in.c_str(),buff); std::string out(buff); delete [] buff; return out; } int main() { list<int> coll; INSERT_ELEMENTS(coll,1,6); PRINT_ELEMENTS(coll,"Исходная коллекция:\n"); // Вычисление суммы произведений элементов // (0 + 1*1 + 2*2 + 3*3 + 4*4 + 5*5 + 6*6) cout << ToRus("Вычисление (0 + 1*1 + 2*2 + 3*3 + 4*4 + 5*5 + 6*6): ") << inner_product (coll.begin(), coll.end(), // Первый интервал coll.begin(), // Второй интервал 0) // Начальное значение << endl; // Вычисление суммы 1*6 ... 6*1 // (0 + 1*6 + 2*5 + 3*4 + 4*3 + 5*2 + 6*1) cout << ToRus("Вычисление (0 + 1*6 + 2*5 + 3*4 + 4*3 + 5*2 + 6*1): ") << inner_product (coll.begin(), coll.end(), // Первый интервал coll.rbegin(), // Второй интервал 0) // Начальное значение << endl; // Вычисление произведения сумм элементов // (1 * 1+1 * 2+2 * 3+3 * 4+4 * 5+5 * 6+6) cout << ToRus("Вычисление (1 * 1+1 * 2+2 * 3+3 * 4+4 * 5+5 * 6+6): ") << inner_product (coll.begin(), coll.end(), // Первый интервал coll.begin(), // Второй интервал 1, // Начальное значение multiplies<int>(), // Внутренняя операция plus<int>()) // Внешняя операция << endl; getch(); return 0; } //---------------------------------------------------------------------------
Результат выполнения программы выглядит так:
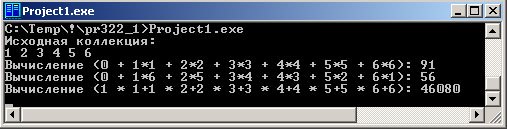
Рис.1. Результат работы приложения
Со следующего шага мы будем рассматривать преобразования относительных и абсолютных значений.
