На этом шаге мы приведем пример использования класса complex.
Следующая программа демонстрирует возможности класса complex по созданию комплексных чисел, их выводу в разных представлениях и выполнению некоторых типовых операций с комплексными числами.
//--------------------------------------------------------------------------- #include <vcl.h> #include <iostream> #include <complex> #include <conio.h> //необходимо для getch() #pragma hdrstop //--------------------------------------------------------------------------- #pragma argsused using namespace std; std::string ToRus(const std::string &in) { char *buff = new char [in.length()+1]; CharToOem(in.c_str(),buff); std::string out(buff); delete [] buff; return out; } int main (int argc, char* argv[]) { // Комплексное число с вещественной и мнимой частями // - Вещественная часть: 4.0 // - Мнимая часть: 3.0 complex<double> c1(4.0,3.0); // Создание комплексного числа в системе полярных координат // - Амплитуда: 5.0 // - Фазовый угол: 0.75 complex<float> c2(polar(5.0,0.75)); // Вывод комплексного числа с вещественной и мнимой частями cout << "c1: " << c1 << endl; cout << "c2: " << c2 << endl; // Вывод комплексного числа в полярных координатах cout << "c1: " <<ToRus("магнитуда: ") << abs(c1) << ToRus(" (квадрат магнитуды: ") << norm(c1) << ") " << ToRus(" фазовый угол: ") << arg(c1) << endl; cout << "c2: " <<ToRus("магнитуда: ") << abs(c2) << ToRus(" (квадрат магнитуды: ") << norm(c2) << ") " << ToRus(" фазовый угол: ") << arg(c2) << endl; // Вывод сопряжений комплексных чисел cout << "c1 " << ToRus("сопряженное число: ") << conj(c1) << endl; cout << "c2 " << ToRus("сопряженное число: ") << conj(c2) << endl; // Вывод результата вычисления cout << "4.4 + c1 * 1.8: " << 4.4 + c1 * 1.8 << endl; // Вывод суммы c1 и c2: // - внимание: разные типы! cout << "c1 + c2: " << c1 + complex<double>(c2.real(),c2.imag()) << endl; // Прибавление к с1 квадратного корня из c1 и вывод результата cout << "c1 += sqrt(c1): " << (c1 += sqrt(c1)) << endl; getch(); return 0; } //---------------------------------------------------------------------------
Примерный результат выполнения программы выглядит так (точный результат зависит от реализации некоторых свойств типа double):
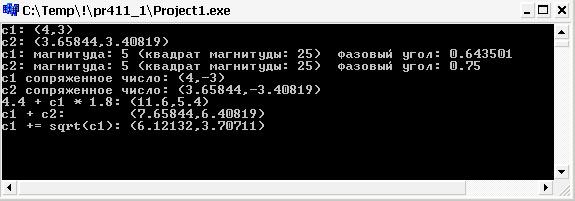
Рис.1. Результат работы приложения
На следующем шаге мы рассмотрим еще один пример использования этого класса.
