На этом шаге мы рассмотрим основные определения, связанные с этим понятием.

Определение [1, с.352] (содержательное).

1. Дерево - это конечное множество T, состоящее из одного или более элементов (называемых вершинами или  узлами), таких, что:
   • имеется одна выделенная вершина, называемая корнем;
   • остальные вершины (исключая корень) содержатся в m ≥ 0 попарно непересекающихся множествах вершин T₁, T₂, ..., T_m, каждое из которых в свою очередь является деревом.
2. Поддеревьями данного дерева называются деревья T₁, T₂, ..., T_m.
3. Упорядоченным деревом будем называть дерево, в котором важен порядок следования поддеревьев T₁, T₂, ..., T_m.

    Приведённое неформальное индуктивное определение является наиболее естественным, т.к. именно рекурсивность является естественной характеристикой структур типа "дерево".

Определение ([1, с.352]) (содержательное).

1. Дуга - это ориентированная связь между двумя вершинами дерева, поэтому, например, корень можно определить как такую вершину дерева, в который не входит ни одной дуги (часто говорят, что корень - это "исходная" вершина дерева, через которую доступны остальные его вершины).
2. Ребро - это неориентированная связь между двумя вершинами дерева. Ребро можно превратить в дугу, если задать на нём ориентацию (направление), а любое дерево можно превратить в ориентированное дерево, если задать ориентацию рёбер.
3. Степенью вершины называется количество её поддеревьев.
4. Сильно ветвящимися деревьями называются деревья, имеющие степень большую 2.
5. Листом называется вершина, имеющая нулевую степень. Другими словами, лист - это вершина бинарного дерева, из которой не выходит ни одной дуги или ребра.
6. Внутренней вершиной (узлом) называется вершина, не являющаяся листом.
7. Весом дерева называется количество листьев дерева.
8. Метками вершин называются символы, используемые для обозначения вершин дерева.

    Для удобства дальнейших рассмотрений договоримся о графическом способе изображения деревьев. Корень будем располагать выше поддеревьев (ясно, что корень при изображении будет располагаться выше всех остальных вершин дерева). Вершины дерева будем изображать точками на плоскости, а корень дерева связывать дугами (ребрами) с корнями деревьев T₁, T₂, ..., T_m.

    Взгляните на рисунок и на комментарии, приведённые ниже его:

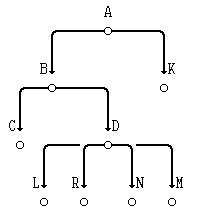
Рис.1. Пример дерева

Определение (содержательное).

Вершина Y, которая находится непосредственно под узлом X, называется (непосредственным) потомком (сыном) X, вершина X в данном случае называется (непосредственным) предком (отцом) Y.

Если вершина X в этом случае находится на уровне i, то говорят, что вершина Y находится на уровне   i+1. Будем считать, что корень дерева расположен на уровне 0.

Глубиной  (высотой)  вершины называется её максимальный уровень.

Степенью дерева называется максимальная степень всех вершин дерева.

    Максимальное число вершин в дереве заданной высоты h достигается, если все вершины имеют по d поддеревьев, кроме вершин уровня h, не имеющих ни одного. Тогда в дереве степени d нулевой уровень содержит одну вершину (корень), первый уровень - d её потомков, второй уровень - d² потомков d узлов уровня 2 и т.д.

    Таким образом получаем, что максимальное число вершин для дерева с высотой h и степенью d можно найти по формуле:

   N(d,h) = 1 + d + d2 + ... + dh.

    При d=2 мы получаем:

   N(2,h) = 1 + 2 +22 + ...  + 2h = 2h+1 - 1.

Определение (содержательное).

1. Ветвью называется путь (последовательность дуг или рёбер) от корня дерева к любому её листу.
2. Длиной пути к вершине X называется количество дуг, которые нужно пройти, чтобы переместиться от корня к вершине X.

    Очевидно, что вершина дерева, расположенная на уровне i, имеет длину пути к этой вершине, равную i.

Определение ([1, с.450]) (содержательное).

Длина (внутреннего) пути дерева определяется как сумма длин путей ко всем его вершинам.

    Для иллюстрации определений приведём рисунок двух упорядоченных деревьев (дерево II отличается от дерева I, т.к. в нём изменён порядок следования поддеревьев с корнями K и B):

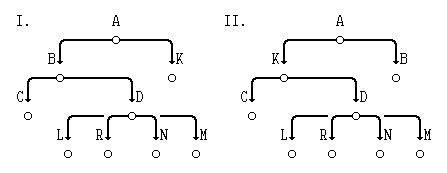
Рис.2. Примеры упорядоченных деревьев

    В дереве II:

• одна из ветвей дерева - AKDL;
• длина пути к вершине L равна 3;
• длина пути к вершине K равна 1;
• длина внутреннего пути равна 18.

    На следующем шаге мы рассмотрим лес.

Предыдущий шаг Содержание Следующий шаг