На этом шаге мы рассмотрим различные представления бинарных деревьев.
Воспользуемся двумя способами описания типа данных "бинарное дерево", опирающихся на одинаковые списочное представление дерева.
Бинарное дерево описательно представим так:
(Корень Левое_поддерево Правое_поддерево)
Для моделирования этого представления в языке Haskell воспользуемся тернарным функтором
(Node root left right),
Таким образом, определение типа данных "целочисленное бинарное дерево" в языке Haskell, поддерживающего класс типов Eq, над которыми определены отношения равенства, будет таким:
data BTree = NIL | Node Int (BTree) (BTree)
deriving Eq
Пример.
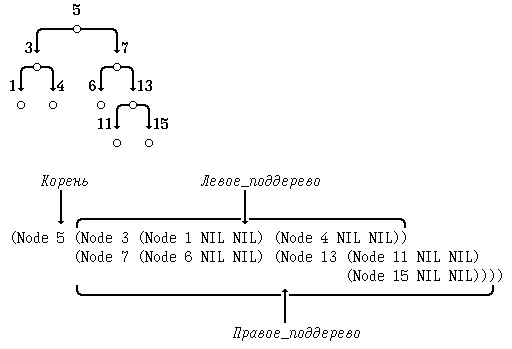
Рис.1. Пример бинарного дерева
Рассмотрим несколько демонстрационных примеров.
-- Демонстрация варианта реализации удаления узла -- из бинарного дерева поиска -- [1, с.192-194] -- ************************* import Tree ----------------------------------------------------- -- Функция, удаляющая узел из бинарного дерева поиска ----------------------------------------------------- deleteTree:: Int -> BTree -> BTree deleteTree e Nil = nil deleteTree e (Node x l r) | e<x = node x (deleteTree e l) r | e==x = join l r | e>x = node x l (deleteTree e r) ------------------------------------------------------------ -- Вспомогательная функция для функции deleteTree ------------------------------------------------- join:: BTree -> BTree -> BTree join Nil b2 = b2 join b1 b2 = node x b1' b2 where (x,b1') = largest b1 ------------------------------------------- -- Вспомогательная функция для функции join ------------------------------------------- largest:: BTree -> (Int,BTree) largest (Node x b1 Nil) = (x,b1) largest (Node x b1 b2) = (y,node x b1 b2') where (y,b2') =largest b2 -- *************************** -- Неудачные тестовые примеры: ------------------------------------ test1 = deleteTree 5 (list 5) == Nil && deleteTree 10 (node 10 (node 4 nil (node 6 (list 5) (node 8 (list 7) (list 9)))) (list 12)) == node 9 (node 4 nil (node 6 (list 5) (node 8 (list 7) nil))) (list 12) ----------------------------- && deleteTree 10 (Node 10 Nil (Node 14 (Node 12 (Node 11 Nil Nil) (Node 13 Nil Nil)) (Node 15 Nil Nil))) == Node 14 (Node 12 (Node 11 Nil Nil) (Node 13 Nil Nil)) (Node 15 Nil Nil) ------------------------------------------------ && deleteTree 2 (Node 4 (Node 2 (Node 1 Nil Nil) (Node 3 Nil Nil)) (Node 6 Nil Nil)) == Node 4 (Node 1 Nil (Node 3 Nil Nil)) (Node 6 Nil Nil) ------------------------------------------------ && deleteTree 4 (Node 4 (Node 2 (Node 1 Nil Nil) (Node 3 Nil Nil)) (Node 6 Nil Nil)) == Node 3 (Node 2 (Node 1 Nil Nil) Nil) (Node 6 Nil Nil) -------------------------------------- && deleteTree 7 (Node 5 Nil (Node 10 (Node 7 (Node 6 Nil Nil) (Node 8 Nil (Node 9 Nil Nil))) Nil)) == Node 5 Nil (Node 10 (Node 6 Nil (Node 8 Nil (Node 9 Nil Nil))) Nil) ----------------------------------------------------------- -- Сравнение результатов работы функций delete и deleteTree ----------------------------------------------------------- test2 = deleteTree 10 (Node 10 (Node 4 Nil (Node 6 (Node 5 Nil Nil) (Node 8 (Node 7 Nil Nil) (Node 9 Nil Nil)))) Nil) test3 = delete 10 (Node 10 (Node 4 Nil (Node 6 (Node 5 Nil Nil) (Node 8 (Node 7 Nil Nil) (Node 9 Nil Nil)))) Nil)
import Tree ----------------------------------------------------------- -- Функция возвращает сумму значений, хранящихся в вершинах -- числового бинарного дерева поиска tree ----------------------------------------- summa:: BTree -> Int summa tree | tree==Nil = 0 | True = root tree + summa (left tree) + summa (right tree) ----------------------------------------------------------- -- Функция возвращает сумму значений, хранящихся в вершинах -- числового бинарного дерева поиска tree -- (с использованием сопоставления с образцом) ---------------------------------------------- summa':: BTree -> Int summa' Nil = 0 summa' (Node x l r) = x + summa' l + summa' r ---------------------------------------------------------- -- Функция, которая в числовом бинарном дереве поиска уве- -- личивает на 1 значения, находящиеся в вершинах ------------------------------------------------- tInc:: BTree -> BTree tInc tree | tree==Nil = Nil | True = Node (1 + root tree) (tInc $ left tree) (tInc $ right tree) ---------------------------------------------------------- -- Функция, которая в числовом бинарном дереве поиска уве- -- личивает на 1 значения, находящиеся в вершинах -- (с использованием сопоставления с образцом) ---------------------------------------------- tInc':: BTree -> BTree tInc' Nil = Nil tInc' (Node x l r) = Node (1+x) (tInc' l) (tInc' r) ----------------------------------------------------- -- Функция, возвращающая "листьевую ширину" числового -- бинарного дерева поиска, т.е. разность между самым -- правым и самым левым листьями дерева --------------------------------------- width:: BTree -> Int width tree = rightList tree - leftList tree ----------------------------------------------------- -- Функция, возвращающая "ширину" числового бинарного -- дерева поиска, т.е. разность наибольшого и наимень- -- шего элемента дерева ------------------------ widthTree:: BTree -> Int widthTree tree = ud tree - ud' tree ------------------------------------------------- -- Функция, возвращающая список листьев бинарного -- дерева поиска ----------------------- leaves:: BTree -> [Int] leaves Nil = [] leaves (Node x l r) | l==Nil && r==Nil = [x] | True = leaves l ++ leaves r -------------------------------------------------------------- -- Функция, присоединяющая бинарное дерево поиска tree1 вместо -- заданного листа x другого бинарного дерева поиска tree -- (полученное дерево уже может не быть деревом поиска!) -------------------------------------------------------- mountTree:: BTree -> BTree -> Int -> BTree mountTree Nil tree1 a = nil mountTree (Node x l r) tree1 a | a==x = tree1 | a<x = node x (mountTree l tree1 a) r | True = node x l (mountTree r tree1 a) -------------------------------------------------------------- -- Функция, присоединяющая бинарное дерево поиска tree1 вместо -- заданного листа x другого бинарного дерева поиска tree -- (полученное дерево уже может не быть деревом поиска!) -------------------------------------------------------- mount':: BTree -> BTree -> [Int] -> BTree mount' tree tree1 [] = tree mount' tree tree1 (x:lst) = mount' (mountTree tree tree1 x) tree1 lst -- *********************************** -- Неудачные тестовые примеры: ------------------------------ test = testSum && testTInc ---------------------------------------------------------- testSum = summa Nil == 0 && summa (Node 10 Nil Nil) == 10 && summa (Node 3 (Node 2 Nil Nil) (Node 4 Nil Nil)) == 9 && summa (Node 4 (Node 2 Nil (Node 3 Nil Nil)) (Node 6 (Node 5 Nil Nil) (Node 7 Nil Nil))) == 27 && summa (Node 10 (Node 6 (Node (-27) Nil Nil) (Node 7 Nil (Node 8 Nil Nil))) (Node 15 (Node 12 Nil Nil) (Node 18 (Node 17 Nil Nil) Nil))) == 66 ---------------------------------------------------------- testTInc = tInc (Node 3 Nil Nil) == Node 4 Nil Nil && tInc (Node 3 (Node 5 Nil Nil) (Node 4 Nil Nil)) == Node 4 (Node 6 Nil Nil) (Node 5 Nil Nil) && tInc (Node 4 (Node 2 Nil (Node 3 Nil Nil)) (Node 6 (Node 5 Nil Nil) (Node 7 Nil Nil))) == Node 5 (Node 3 Nil (Node 4 Nil Nil)) (Node 7 (Node 6 Nil Nil) (Node 8 Nil Nil)) ------------------------------------------------------- tree = node 10 (node 6 (list 3) (node 7 nil (list 8))) (node 15 (list 12) (node 18 (list 17) nil)) tree1 = node 10 (node 6 (list (-27)) (node 7 nil (list 8))) (node 15 (list 12) (node 18 (list 17) nil)) tree2 = node (-1) (list (-1)) (list (-1)) ----------------------------------------- test1 = leaves tree; test2 = leaves tree1 ----------------------------------------- test3 = outTree tree; test4 = width tree test5 = outTree tree1; test6 = width tree1 ------------------------------------------ test7 = do outTree tree putStr ("\n"++"Rezult: "++show (widthTree tree)++"\n") ---------------------------------------------------------------- test8 = outTree tree1; test102 = widthTree tree1 ------------------------------------------------ test9 = widthTree (list 5) -------------------------------------------------------------- test10 = outTree (mountTree (mountTree tree tree2 8) tree2 17) test11 = outTree (mount' tree tree2 (leaves tree))
import Tree --------------------------------------------------------- -- Функция, удаляющая из бинарного дерева поиска все вер- -- шины, расположенные на уровнях, больших заданного k ------------------------------------------------------ tCopy' k Nil = Nil tCopy' k tree | topNode (root tree) tree==k = list (root tree) | True = node (root tree) (tCopy' (k-1) (left tree)) (tCopy' (k-1) (right tree)) --------------------------------------------------------------- -- Функция, возвращающая список вершин бинарного дерева поиска, -- находящихся на заданном уровне k (при вызове tree1:=tree) ------------------------------------------------------------ levelTree:: Int -> BTree -> BTree -> [Int] levelTree k tree tree1 | tree==Nil = [] | True = levelTree k (left tree) tree1 ++ (f (root tree) tree1) ++ levelTree k (right tree) tree1 where f x tree | topNode x tree==k = [x] | True = [] -------------------------------------------------------------- -- Предикат, устанавливающий, что бинарное дерево поиска tree1 -- является поддеревом бинарного дерева поиска tree2 ---------------------------------------------------- subTree:: BTree -> BTree -> Bool subTree tree1 tree2 | isEmpty tree1 || isEmpty tree1 && isEmpty tree2 = True | isEmpty tree2 = False | True = root tree1==root tree2 && subTree (left tree1) (left tree2) && subTree (right tree1) (right tree2) ------------------------------------------------------------- -- Предикат, распознающий бинарное дерево поиска tree ----------------------------------------------------- isBTree:: BTree -> Bool isBTree tree | isEmpty tree = True | isEmpty (left tree) && isEmpty (right tree) = True | isEmpty (left tree) = root tree<root (right tree) && isBTree (right tree) | isEmpty (right tree) = root tree>root (left tree) && isBTree (left tree) | True = root tree>root (left tree) && root tree<root (right tree) && isBTree (left tree) && isBTree (right tree) -- ************************************************* -- Неудачные тестовые примеры: -------------------------------- tree = node 10 (node 6 (list 3) (node 7 nil (list 8))) (node 15 (list 12) (node 18 (list 17) nil)) tree1 = node 5 (node 3 (list 1) (list 4)) (node 7 (list 6) (node 9 (list 8) (list 15))) tree2 = newRndTree 4 44 9 ---------------------------------------------- test1 = putStr( show (tCopy' 0 tree) ++ "\n" ++ show (tCopy' 1 tree) ++ "\n" ++ show (tCopy' 2 tree) ++ "\n" ++ show (tCopy' 3 tree) ++ show (tCopy' 4 tree) ++ "\n") ----------------------------------------------- test2 = levelTree 0 tree tree == [10] && levelTree 1 tree tree == [6,15] && levelTree 2 tree tree == [3,7,12,18] && levelTree 3 tree tree == [8,17] && levelTree 4 tree tree == [] ----------------------------------------- test3 = levelTree 0 tree1 tree1 == [5] && levelTree 1 tree1 tree1 == [3,7] && levelTree 2 tree1 tree1 == [1,4,6,9] && levelTree 3 tree1 tree1 == [8,15] && levelTree 4 tree1 tree1 == [] ---------------------------------------- test31 = levelTree 0 tree1 tree1 ++ levelTree 1 tree1 tree1 ++ levelTree 2 tree1 tree1 ++ levelTree 3 tree1 tree1 ++ levelTree 4 tree1 tree1 -------------------------------------- test4 = subTree (tCopy' 0 tree) tree && subTree (tCopy' 1 tree) tree && subTree (tCopy' 2 tree) tree && subTree (tCopy' 3 tree) tree --------------------------------- && subTree (tCopy' 2 tree2) tree2 && subTree (tCopy' 3 tree2) tree2 ------------------------------------------------------ test5 = isBTree tree && isBTree tree1 && isBTree tree2 ------------------------------------------------------ tree3 = node 10 (node 6 (list 3) (node 17 nil (list 8))) (node 15 (list 12) (node 18 (list 17) nil)) tree4 = node 10 (node 6 (list 3) (node 7 nil (list 8))) (node 1 (list 12) (node 18 (list 17) nil)) test6 = outTree tree4 test7 = not (isBTree tree3) && not (isBTree tree4) test8 = isBTree tree1 && isBTree tree2
import Tree ------------------------------------------------------ -- Предикат, устанавливающий наличие пути от вершины a -- до вершины b бинарного дерева поиска tree -------------------------------------------- way_AB:: Int -> Int -> BTree -> Bool way_AB a b tree = search a (search b tree)/=nil || search b (search a tree)/=nil -------------------------------------------------------- -- Функция, возвращающая длину пути от корня до заданной -- вершины a в бинарном дереве поиска tree ------------------------------------------ lenWay:: Int -> BTree -> Int lenWay a tree | isEmpty tree || root tree==a = 0 | a<root tree = 1 + lenWay a (left tree) | True = 1 + lenWay a (right tree) ------------------------------------------------------- -- Функция, возвращающая все пути в заданном бинарном -- дереве поиска ----------------------------------- allWays:: BTree -> BTree -> [[Int]] allWays tree tree1 | isEmpty tree = [] | True = allWays (left tree) tree1 ++ [waySearch (root tree) tree1] ++ allWays (right tree) tree1 ---------------------------------------------------- -- Функция, возвращающая путь к заданной вершине -- в бинарном дереве поиска --------------------------------- waySearch:: Int -> BTree -> [Int] waySearch a Nil = [] waySearch a (Node x l r) | a==x = [x] | a<x = [x] ++ waySearch a l | True = [x] ++ waySearch a r ------------------------------------------------------ -- Функция возвращает минимальное расстояние от корня -- бинарного дерева поиска Tree до листьев ------------------------------------------ abc:: BTree -> Int abc tree | isEmpty (left tree) && isEmpty (right tree) = 0 | isEmpty (left tree) = 1 + abc (right tree) | isEmpty (right tree) = 1 + abc (left tree) | True = min (1 + abc (left tree)) (1 + abc (right tree)) ------------------------------------------------------------ -- Функция возвращает "отца" для заданной вершины x -- бинарного дерева поиска tree ------------------------------- srchFath':: Int -> BTree -> Int srchFath' x tree = last (init (waySearch x tree)) ------------------------------------------------- -- Функция, возвращающая длину внутреннего пути -- в бинарном дереве поиска Tree. -- -- Длина внутреннего пути = -- ¦0, если дерево пусто; -- ¦-1 + Количество узлов в дереве -- ¦ + Длина внутреннего пути левого поддерева -- ¦ + Длина внутреннего пути правого поддерева ---------------------------------------------------- interWay:: BTree -> Int interWay tree | isEmpty (tree) = 0 | True = -1 + length (klpObh tree) + interWay (left tree) + interWay (right tree) -- ******************************************************** -- Неудачные тестовые примеры: ---------------------------------------- test = testWay_AB && testLenWay && test1 ----------------------------------------------------- testWay_AB = way_AB 1 2 (Node 1 (Node (-1) Nil Nil) (Node 2 Nil Nil)) == True && way_AB 10 22 (Node 8 (Node 6 (Node 1 Nil Nil) Nil) (Node 10 Nil (Node 14 (Node 12 Nil Nil) (Node 22 Nil Nil)))) == True && way_AB 2 5 (Node 3 (Node 5 Nil Nil) (Node 4 Nil Nil)) == False && way_AB 2 7 (Node 4 (Node 2 Nil Nil) (Node 6 (Node 5 Nil Nil) (Node 7 Nil Nil))) == False && way_AB 3 7 (Node 4 (Node 2 Nil (Node 3 Nil Nil)) (Node 6 (Node 5 Nil Nil) (Node 7 Nil Nil))) == False ------------------------------------------------------- testLenWay = lenWay 3 (list 3) == 0 && lenWay 3 (node 5 (list 3) (list 4)) == 1 && lenWay 5 (node 4 (node 2 nil (list 3)) (node 6 (list 5) (list 7))) == 2 && lenWay 7 (node 4 (node 2 nil (list 3)) (node 6 (list 5) (list 7))) == 2 && lenWay 3 (node 9 (node 6 (list 3) (node 7 nil (list 8))) (node 15 (list 12) (node 18 (list 17) nil))) == 2 ----------------------------------------------------------- test1 = interWay (Node 3 Nil Nil) == 0 && interWay (Node 3 (Node 5 Nil Nil) (Node 4 Nil Nil)) == 2 && interWay (Node 4 (Node 2 Nil (Node 3 Nil Nil)) (Node 6 (Node 5 Nil Nil) (Node 7 Nil Nil))) == 8 && interWay (Node 10 (Node 6 (Node 3 Nil Nil) (Node 7 Nil (Node 8 Nil Nil))) (Node 15 (Node 12 Nil Nil) (Node 18 (Node 17 Nil Nil) Nil))) == 16 ------------------------------------------------------------ tree = node 10 (node 6 (list 3) (node 7 nil (list 8))) (node 15 (list 12) (node 18 (list 17) nil)) tree1 = node 10 (node 6 (list (-27)) (node 7 nil (list 8))) (node 15 (list 12) (node 18 (list 17) nil)) ------------------------------------------------- test2 = waySearch 8 tree test3 = allWays tree tree test4 = srchFath' 3 (node 4 (list 3) (list 5)) == 4 && srchFath' 5 (Node 4 (Node 3 Nil Nil) (Node 5 Nil Nil)) == 4 && srchFath' 5 (Node 4 (Node 2 Nil (Node 3 Nil Nil)) (Node 6 (Node 5 Nil Nil) (Node 7 Nil Nil))) == 6 && srchFath' 6 (Node 4 (Node 2 Nil (Node 3 Nil Nil)) (Node 6 (Node 5 Nil Nil) (Node 7 Nil Nil))) == 4 && srchFath' 17 (Node 10 (Node 6 (Node 3 Nil Nil) (Node 7 Nil (Node 8 Nil Nil))) (Node 15 (Node 12 Nil Nil) (Node 18 (Node 17 Nil Nil) Nil))) == 18 && srchFath' 7 (Node 10 (Node 6 (Node 3 Nil Nil) (Node 7 Nil (Node 8 Nil Nil))) (Node 15 (Node 12 Nil Nil) (Node 18 (Node 17 Nil Nil) Nil))) == 6 ----------------------------------------------------------- test5 = abc tree test6 = abc tree1
Представим также описание полиморфного типа данных "Бинарное дерево" [2]:
data BTree a = Empty | Node (a, BTree a, BTree a)
Функтор Empty задаёт пустое дерево. Функтор Node задаёт описание вершины a бинарного дерева с указанием исходящих из неё левого и правого поддеревьев.
Пример.
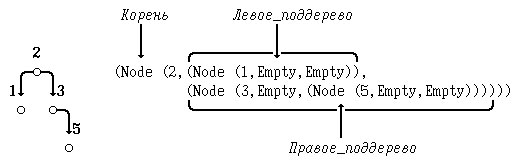
Рис.2. Пример полиморфного типа данных "Бинарное дерево"
(1)Роганова Н.А. Функциональное программирование. - М: ГИНФО, 2002. - 260 с.
(2)Душкин Р.В. Функциональное программирование на языке Haskell. - М.: ДМК Пресс, 2007. - 608 с.
На следующем шаге мы рассмотрим бинарные дерева поиска с ключами.
