На этом шаге мы приведем задачи для самостоятельного решения.
Замечание. Найдите ошибки, описки, неточности и прочие изъяны в приведенных задачах.
1. Построение бинарного дерева поиска
1*. Напишите функцию, которая строит копию заданного бинарного дерева поиска.
2*. Напишите функцию, которая по заданному бинарному дереву поиска строит новое бинарное дерево поиска, состоящее из листьев исходного дерева.
3*. Напишите функцию, последовательно помещающую целые числа из одноуровневого списка в бинарное дерево поиска.
4*. Напишите функцию, последовательно помещающую целые числа из одноуровневого списка в бинарное дерево поиска. На основе этого представления упорядочите элементы списка по убыванию.
5*. Напишите функцию, последовательно помещающую целые числа из одноуровневого списка в бинарное дерево поиска. На основе этого представления упорядочите элементы списка по возрастанию.
6*. Напишите функцию построения бинарного дерева поиска для заданного одноуровневого списка целых чисел и занумеруйте его вершины в соответствии с их порядком:
- при обратном обходе дерева (ЛКП);
- при "зеркальном" обратном обходе дерева (ПКЛ).
7*. Напишите функцию построения бинарного дерева поиска для заданного одноуровневого списка целых чисел и занумеруйте его вершины в соответствии с их порядком:
- при концевом обходе дерева (ЛПК);
- при "зеркальном" концевом обходе дерева (ПЛК).
8*. Напишите функцию построения бинарного дерева поиска для заданного одноуровневого списка целых чисел и занумеруйте его вершины в соответствии с их порядком:
- при левостороннем обходе дерева (КЛП);
- при правостороннем обходе дерева (КПЛ).
9*. Напишите функцию, осуществляющую вывод на экран бинарного дерева поиска в виде "обычного" дерева, перевёрнутого корнем вверх.
10*. Напишите функцию построения бинарного дерева поиска, элементы которого вводятся в соответствии с их расположением по уровням дерева.
Указание. Воспользуйтесь следующим алгоритмом, pеализующим обход деpева в шиpину, используя две очеpеди O1 и O2:
Взять пустые очеpеди O1 и O2;
Поместить коpень в очеpедь O1;
While Одна из очеpедей O1 и O2 не пуста do
If O1 не является пустой
then begin
Пусть p - узел, находящийся в голове очеpеди O1;
Посетить веpшину p и удалить ее из O1;
Поместить всех сыновей веpшины p в очеpедь O2,
начиная со стаpшего сына
end
else В качестве O1 взять непустую очеpедь O2, а
в качестве O2 взять пустую очеpедь O1
11*. Напишите функцию построения бинарного дерева поиска по результатам нисходящего и смешанного обходов.
12*. Напишите функцию построения бинарного дерева поиска по результатам смешанного и восходящего обходов.
2. Модификация бинарного дерева поиска
1*. Напишите функцию, которая добавляет к бинарному дереву поиска вершину, содержащую новый элемент, если его не было в дереве.
2*. Напишите функцию, которая в заданном бинарном дереве поиска, содержащем целые числа, увеличивает на единицу значения, находящиеся в вершинах.
3*. Напишите функцию, которая удаляет из бинарного дерева поиска, содержащего целые числа, все вершины:
- с положительными значениями;
- с отрицательными значениями;
- с чётными значениями;
- с нечётными значениями.
4. Напишите функцию, которая удаляет из бинарного дерева поиска, содержащего целые числа, вершины с максимальным и минимальным элементами.
5. Напишите функцию, которая удаляет из бинарного дерева поиска самые крайние листья дерева.
6. Напишите функцию, которая удаляет из бинарного дерева поиска "центральные" листья дерева.
7. Напишите функцию, которая один раз удаляет листья из бинарного дерева поиска.
8. Напишите функцию, преобразующую бинарное дерево поиска Tree в бинарное дерево поиска с добавленными к листьям дерева Tree фиктивными узлами d с NIL-указателями.
9*. Напишите функцию, реализующую операцию "правая ротация в бинарном дереве поиска" по следующему рисунку:
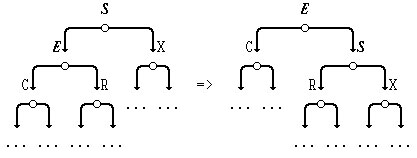
10*. Напишите функцию, реализующую операцию "левая ротация в бинарном дереве поиска" по следующему рисунку:
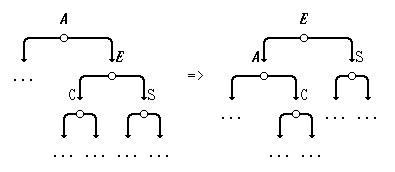
3. Предикаты над бинарными деревьями поиска
1**. Напишите предикат, проверяющий, входит ли вершина, содержащая заданное целое число, в заданное числовое бинарное дерево поиска.
2*. Напишите предикат, проверяющий, входит ли вершина, содержащая заданное целое число, в правое или левое поддерево заданного числового бинарного дерева поиска.
3*. Напишите предикат, проверяющий на равенство заданные бинарные деревья поиска.
4*. Напишите предикат, проверяющий на равенство левые поддеревья двух заданных бинарных деревьев поиска.
5*. Напишите предикат, проверяющий на равенство правые поддеревья двух заданных бинарных деревьев поиска.
6*. Напишите предикат, проверяющий, совпадают ли элемент из самого правого листа числового бинарного дерева поиска с квадратом элемента из самого левого листа.
7*. Напишите предикат, устанавливающий, можно ли попасть из одной заданной вершины бинарного дерева поиска в другую заданную вершину, если двигаться в направлении от корня к листьям.
8*. Заданы бинарное дерево поиска и две его вершины A и B. Напишите предикат, определяющий входит ли вершина A в левое поддерево дерева с корнем B.
9*. Напишите предикат, определяющий, совпадает ли сумма информационных полей листьев с информационным полем корня заданного бинарного дерева поиска.
91. Напишите функцию, определяющую, является ли заданная вершина бинарного дерева поиска правым (левым) "сыном" некоторой вершины.
10*. Напишите предикат, распознающий изоморфизм двух данных бинарных деревьев.
11*. Напишите предикат, распознающий подобие двух данных бинарных деревьев.
12*. Напишите предикат, распознающий эквивалентность двух данных бинарных деревьев.
13*. Напишите функцию, определяющую вхождение заданного бинарного дерева поиска в другое бинарное дерево поиска.
4. Определение вершин бинарного дерева поиска, обладающих заданными свойствами
1**. Напишите функцию, которая определяет максимальный элемент из всех листьев заданного числового бинарного дерева поиска.
2**. Напишите функцию, которая определяет минимальный элемент из всех листьев заданного числового бинарного дерева поиска.
3**. Напишите функцию, которая определяет количество элементов левого поддерева заданного бинарного дерева поиска.
4**. Напишите функцию, которая определяет количество элементов правого поддерева заданного бинарного дерева поиска.
41*. Определите какое из поддеревьев заданного бинарного дерева поиска имеет большее количество листьев.
5*. Напишите функцию, которая вычисляет сумму элементов всех вершин числового бинарного дерева поиска.
6*. Напишите функцию, которая вычисляет произведение элементов всех вершин числового бинарного дерева поиска.
7*. Напишите функцию, которая вычисляет среднее арифметическое элементов числового бинарного дерева поиска.
8**. Напишите функцию для определения высоты бинарного дерева поиска.
Указание. Высотой бинарного дерева поиска называется количество его уровней.
81. Напишите функцию для определения ширины бинарного дерева поиска.
Указание. Шириной бинарного дерева поиска называется максимальное количество вершин, располагающихся на некотором уровне дерева.
82*. Напишите функцию, определяющую, какое из поддеревьев заданного бинарного дерева поиска имеет большую высоту.
83*. Напишите функцию, определяющую, какое из поддеревьев заданного бинарного дерева поиска имеет большее количество уровней.
84*. Напишите функцию, определяющую какая величина больше: количество листьев в левом поддереве заданного бинарного дерева поиска или количество уровней в его правом поддереве.
9*. Определите количество непустых поддеревьев в заданном бинарном дереве поиска.
10*. Напишите функцию, возвращающую уровень заданной вершины в бинарном дереве поиска.
11*. Напишите функцию, определяющую по заданной вершине бинарного дерева поиска его "сыновей".
111. Напишите функцию, возвращающую левого (правого) "брата" заданного узла в бинарном дереве поиска и NIL, если такового не существует.
112. Напишите функцию, определяющую количество "сыновей" у заданной вершины бинарного дерева поиска.
12*. Напишите функцию, которая определяет максимальную глубину бинарного дерева поиска.
Указание. Максимальной глубиной бинарного дерева поиска называется количество ветвей в самом длинном из путей от корня дерева до листьев.
13*. Напишите функцию, которая находит в бинарном дереве поиска длину пути от корня до вершины с заданным элементом.
131. Напишите функцию, определяющую пути от корня до каждого листа бинарного дерева поиска.
132. Напишите функцию, возвращающую кратчайший путь от заданной вершины бинарного дерева поиска до листьев.
133. Напишите функцию, возвращающую длину кратчайшего пути от заданной вершины бинарного дерева поиска до листьев.
134. Напишите функцию, возвращающую самый длинный путь от заданной вершины бинарного дерева поиска до листьев.
135. Напишите функцию, возвращающую длину самого длинного пути от заданной вершины бинарного дерева поиска до листьев.
14. Напишите функцию для определения высоты бинарного дерева поиска, используя функцию определения длины пути от корня до данной вершины.
15*. Напишите функцию, которая подсчитывает число вершин на n-ом уровне бинарного дерева (корень является вершиной 0-го уровня).
151. Напишите функцию, определяющую в бинарном дереве поиска:
- элемент, следующий за данным;
- элемент, предшествующий данному.
Указание. Определите самостоятельно новые понятия.
152. (По [1, с.241]) Напишите функцию, выводящую все элементы бинарного дерева поиска в неубывающем порядке следующим образом: найдите минимальный элемент, а затем n-1 раз ищите элемент, следующий за ним.
153. Напишите функцию, возвращающую ширину бинарного дерева поиска.
Указание. Шириной бинарного дерева поиска называется разность значений его самого правого и самого левого листа.
154. Напишите функцию, возвращающую для заданной вершины бинарного дерева поиска:
(1) прадеда (great-grandfather); (9) двоюродного брата (cousin); (2) деда (grandfather); (10) двоюродных племянников; (3) отца (father); (11) двоюродных дядей; (4) брата (brother); (12) двоюродных дедов; (5) дядю (uncle); (13) двоюродных внуков; (6) племянников (nephew); (14) троюродных племянников; (7) сыновей (sons); (15) троюродных братьев (8) внуков (grandsons); (second cousins).
Указание.
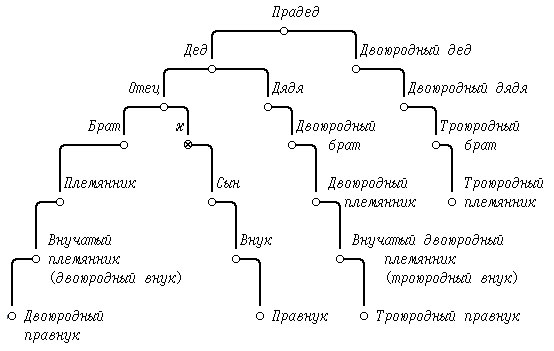
155. (Кенгуру, 1999, 7-8 классы, 5 баллов) Говоря о своём дедушке, Катя каждый раз старалась назвать его по-новому: "отец моего отца", "отец брата моего отца", "отец отца сына моего отца", "отец брата отца моего брата", "брат отца отца моего брата". Сколько раз Катя ошиблась? (Все братья родные!) (Ответ: один раз)
156. (По [2, с.815]) Найдите для каждой пары вершин бинарного дерева поиска ближайшего общего предка.
16*. Напишите функцию для определения суммарного пути бинарного дерева поиска, используя функцию определения пути от корня до данной вершины.
17*. Напишите функцию, которая выводит содержимое всех внутренних вершин данного бинарного дерева поиска.
18*. Напишите функцию для подсчёта количества пустых указателей в программном представлении данного бинарного дерева поиска.
19. Напишите функцию, которая вычисляет среднее геометрическое всех элементов бинарного дерева поиска.
5. Бинарные дерева поиска с ключами
1. Напишите функцию построения бинарного дерева поиска, элементы которого могут повторяться, а, следовательно, поиск информации в дереве осуществляется по ключу.
2. Напишите функцию, которая удаляет все вершины с одинаковыми элементами из бинарного дерева поиска.
3. Напишите функцию, определяющую количество повторяющихся элементов в бинарном дереве поиска.
4. Напишите функцию, которая определяет число вхождений вершины с заданным элементом в бинарное дерево поиска.
5. Напишите функцию, которая выбирает из вершин заданного бинарного дерева поиска все разные элементы и формирует их в список.
6. Напишите предикат, определяющий, входит ли вершина, содержащая заданное число, дважды в числовое бинарное дерево поиска.
7. (По [3, с.519]) Напишите функцию, реализующую "ленивую" стратегию удаления узла из бинарного дерева поиска, которая оставляет удалённые узлы в структуре данных, но помечает их как "удалённые", которые будут игнорироваться при поиске.
Замечание. Помеченные узлы можно использовать в будущих вставках, когда это удобно (например, это можно было бы легко сделать для узлов в нижней части дерева).
8. Напишите функцию, которая находит в бинарном дереве поиска длину пути от корня до ближайшей вершины с заданным элементом.
6. Случайные бинарные деревья поиска
1. Напишите функцию, генерирующую случайные бинарные деревья поиска с заданным количеством вершин.
2. Напишите функцию, генерирующую случайные бинарные деревья поиска с заданным количеством листьев.
3. Напишите функцию, генерирующую случайные бинарные деревья поиска с заданным количеством дуг.
4. Напишите функцию, генерирующую случайные бинарные деревья поиска с заданной высотой (числом уровней).
5. (По [1, с.249]) Проверьте утверждение следующей теоремы: средняя высота случайного бинарного дерева поиска, построенного по n различным вершинам, есть O(log2n).
6. Напишите функцию, генерирующую случайные бинарные деревья поиска с заданной высотой левого (правого) поддерева.
7. Напишите функцию, генерирующую случайные бинарные деревья поиска, имеющие n вершин на заданном k-м уровне.
7. "Кольцевые" бинарные деревья поиска
1*. Напишите функцию, возвращающую бинарное дерево поиска, заданный лист которого содержит указатель на заданную вершину дерева.
2*. Напишите функцию для построения кольцевого бинарного дерева поиска, самый левый лист которого содержит указатель на корень дерева.
8. Типы древовидных структур
1*. Напишите АТД для бинарного дерева поиска, которое содержит информацию о повторяющихся ключах.
2. [4, с.205-206] Пусть дерево задаётся следующим объявлением типа:
data Tree' = Empty | Leaf Int | Node Tree' Int Tree'
deriving (Show)
Приведём несколько примеров деревьев данного типа:
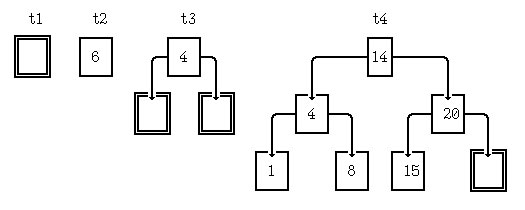
Здесь t1 - пустое дерево, t2 - дерево с единственным элементом (листом), имеющим тип Int, t3 и t4 - примеры многоуровневых деревьев, построенных из внутренних вершин, вершин-листьев и пустых деревьев. Каждая внутренняя вершина содержит число и два поддерева.
Первые три дерева заданы определениями:
t1,t2,t3:: Tree' t1 = Empty t2 = Leaf 16 t3 = Node Empty 4 Empty
- Приведите выражение, описывающее дерево t4.
- Напишите программу, содержащую функции вставки и удаления элементов в дерево типа Tree'.
- Напишите функцию сортировки с помощью дерева типа Tree'.
3. [4, с.206] Дано дерево следующего типа:
data Tree'' = Leaf a | Node'' (Tree'' a) (Tree'' a)
(1) Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. - М.: МЦНМО, 1999. - 960 с.
(2) Уайс М.А. Организация структур данных и решение задач на C++. - М.: ЭКОМ Паблишерз, 2008. - 896 с.
(3) Седжвик Р. Фундаментальные алгоритмы C++. Анализ. Структуры данных. Сортировка. Поиск. - К.: ДиаСофт, 2001. - 688 с.
(4) Роганова Н.А. Функциональное программирование. - М: ГИНФО, 2002. - 260 с.
На следующем шаге мы рассмотрим сбалансированное дерево.
