На этом шаге мы рассмотрим назначение этой операции.
В классической реализации BST-деревьев каждый новый вставляемый узел попадает в дерево в виде листа.
Рассмотрим метод включения [1, с.512-513], при котором каждый новый элемент вставляется в корень, и поэтому недавно включённые узлы находятся вблизи корня дерева.
Воспользуемся операцией "ротация", которая является фундаментальным преобразованием бинарных деревьев поиска и позволяет менять местами корень и один из его дочерних узлов при сохранении порядка ключей в узлах BST-дерева.
Ротация - это локальное изменение дерева, затрагивающее только три связи и два узла; она позволяет перемещать узлы по деревьям, не изменяя глобальных свойств порядка, превращающих BST-дерево в полезную структуру данных, предназначенную для поиска.
1. Операция "ротация вправо" затрагивает корень и левый дочерний узел; она помещает корень справа, изменяя на обратное направление левой связи корня; перед ротацией она указывает от корня к левому дочернему узлу, а после ротации - от левого дочернего узла ("нового" корня) к "старому" корню (правый дочерний узел нового корня).
Основная часть - это копирование правой связи левого дочернего узла, чтобы она стала левой связью "старого" корня. Эта связь указывает на все узлы с ключами между двумя узлами, участвующими в ротации. И наконец, связь со "старым" корнем должна быть изменена так, чтобы указывать на "новый" корень.
Другими словами, операция "ротация вправо" делает "старый" корень корнем правого поддерева "нового" корня.
Пример выполнения операции "правая ротация".
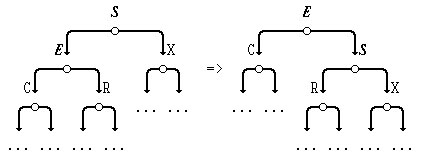
Рис.1. Операция "правая ротация"
2. Описание операции "ротация влево" аналогично приведённому выше определению операции "ротация вправо" с точностью до слов "правый" и "левый".
Другими словами, операция "ротация влево" превращает "старый" корень в корень левого поддерева "нового" корня.
Пример выполнения операции "левая ротация".
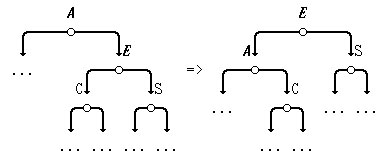
Рис.2. Операция "левая ротация"
Операция "ротация" используется для:
- (1) перемещения заданных узлов "вверх" по дереву;
- (2) для предотвращения разбалансировки деревьев.
(1) Седжвик Р. Фундаментальные алгоритмы C++. Анализ. Структуры данных. Сортировка. Поиск. - К.: ДиаСофт, 2001. - 688 с.
На следующем шаге мы рассмотрим несколько демонстрационных примеров.
