На этом шаге мы введем некоторые общие понятия.
Работа с бинарными деревьями более эффективна тогда, когда деревья сбалансированы, т.е. длина пути от корня до любого из листьев находится в определённых пределах, связанных с числом узлов.
Поиск, включение и удаление узлов в сбалансированном бинарном дереве производится намного быстрее, чем в несбалансированном, скорость обработки которого может быть лишь немного быстрее, чем в линейном списке.
Красно-чёрные деревья - это разновидность бинарных деревьев поиска, использующая эффективный механизм поддержания сбалансированности дерева.
Красно-чёрные деревья были введены R.Bayer [1972], а затем их изучали и разрабатывали L.J.Guibas и R.Sedgewick [1978]. Название происходит от стандартной раскраски узлов таких деревьев в красный и чёрный цвета, используемые для балансировки дерева.
Оценкой среднего (а также и наихудшего) времени поиска в красно-чёрных деревьев, содержащим n узлов, является
O(log2n).
Замечание. В стандартной библиотеке классов языка C++ (STL) исполнители "множество" и "нагруженное множество" (классы set и map) реализованы на базе красно-чёрных деревьев.
- Определение (по [1, с.340]).
- Красно-чёрное дерево - это бинарное дерево поиска со следующими свойствами:
- (1) каждый узел может находится в одном из двух состояний, которые называются красным и чёрным (говорят, что каждый узел окрашен либо в красный, либо в чёрный цвет);
- (2) каждый узел дерева, имеющий хотя бы одну нулевую дочернюю связь, указывает на "несуществующие" узлы, которые называются листьями (внешними узлами, NIL-листьями) и всегда окрашены в чёрный цвет; остальные узлы называются внутренними узлами;
- (3) свойство красного узла: если узел является красным, то оба его потомка являются чёрными (другими словами, каждый красный узел должен иметь чёрного предка);
- (4) свойство чёрного узла: на всех ветвях дерева, ведущих от его корня к листьям, количество чёрных узлов одинаково.
Пункты (3) и (4) определения проверяют, что дерево остаётся в определённом смысле сбалансированным.
Более того, операции включения и удаления в красно-чёрном дереве, использующие правила (3) и (4), гораздо более эффективны, чем аналогичные, использующие полную балансировку (например, как в АВЛ-деревьях).
Примеры красно-чёрных деревьев.
Внешние узлы будем изображать маленькими чёрными квадратами.
1. Пустое красно-чёрное дерево - это бинарное дерево, состоящее всего из одного внешнего чёрного узла:
2. Красно-чёрное дерево с единственным корневым узлом (красным или чёрным):
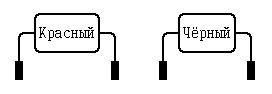
Рис.1. Красно-чёрное дерево с единственным корневым узлом
Итак, красно-чёрное дерево с единственным узлом содержит также два NIL-листа, являющиеся двумя нулевыми связями, исходящими из единственного "реального" внутреннего узла.
3. Красно-чёрное дерево, содержащее два узла, корневой и дочерний (левый или правый), и, соответственно, три листа; оно представимо единственным образом, удовлетворяя определению понятия "красно-чёрное дерево": корневой узел окрашен в чёрный цвет, дочерний узел - в красный цвет, а NIL-листья - в чёрный:
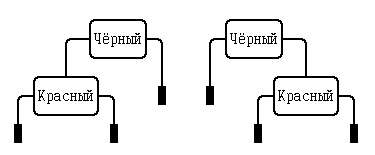
Рис.2. Красно-чёрное дерево, содержащее два узла
Замечание. Существуют бинарные деревья, вершины которых не могут быть окрашены в красный и чёрный цвета по правилам для красно-чёрных деревьев. Из свойства чёрных узлов следует, что пути, ведущие из произвольной вершины x красно-чёрного дерева к листьям, содержат одно и то же количество чёрных вершин, которая называется чёрной высотой вершины x.
Пример дерева, не являющегося красно-чёрным деревом).
Если узел с произвольным цветом (красным или чёрным) пометим меткой "?", то следующее дерево не является красно-чёрным деревом:
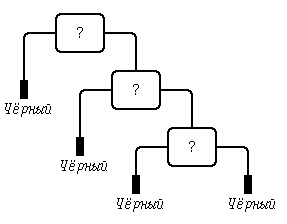
Рис.3. Дерево, не являющееся красно-чёрным
- Определение.
-
- (1) Чёрной высотой вершины x называется количество чёрных вершин в любом пути, ведущем от вершины x к листьям (при этом цвет вершины x не учитывается).
- (2) Чёрной высотой дерева называется чёрная высота корня.
Пример.
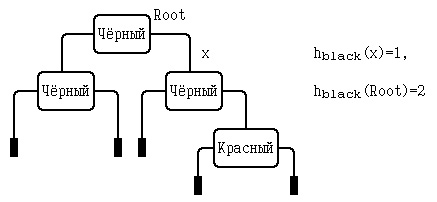
Рис.4. Чёрная высота дерева
Замечание. Самый длинный путь в красно-чёрном дереве от корня к листу не более чем вдвое длиннее любого другого его пути от корня к листу.
Пример. Рассмотрим красно-чёрное дерево с чёрной высотой hblack(Root)=2.
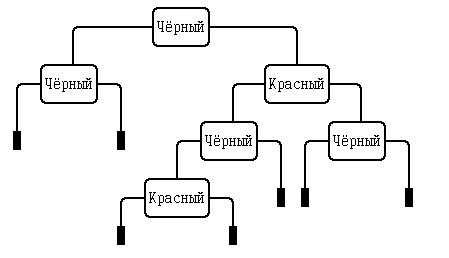
Рис.5. Дерево с чёрной высотой hblack(Root)=2
Кратчайший путь от корня до листа равен 2.
Максимальный путь от корня до листа красно-чёрного дерева с чёрной высотой 2 равен 4 и составляет этот путь последовательность чередования красных и чёрных узлов. Добавление чёрного узла к ветви дерева, представляющей собой длиннейший путь от корня до листа, невозможно, поскольку при этом нарушится свойство чёрного узла.
Добавление красного узла к этой же ветви также недопустимо, т.к. у красных узлов должны быть чёрные потомки.
Таким образом, в данной ситуации самый длинный путь от корня до листа красно-чёрного дерева вдвое длиннее пути, проходящего только через чёрные узлы.
- Лемма [2, с.255].
- Красно-чёрное дерево с n внутренними вершинами (отличными от NIL-листьев) имеет высоту не большую
2log2(n+1).
(1)Бакнелл Д.М. Фундаментальные алгоритмы и структуры данных в Delphi. - СПб.: ООО "ДиаСофтЮП", 2003. - 560 с.
(2)Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. - М.: МЦНМО, 1999. - 960 с.
На следующем шаге мы продолжим рассмотрение этого вопроса.
