На этом шаге мы приведем некоторые общие рассуждения по поводу удаления узла .
Удаление узла вначале выполняется так же, как это делалось в классическом бинарном дереве поиска. Однако затем может потребоваться восстановление свойств красно-чёрных деревьев.
Рассмотрим три случая удаления узла S, учитывая необходимость сохранения свойств красно-чёрного дерева [1, с.348-349]).
1. Оба дочерних узла у узла S являются NIL-узлами (внешними узлами).
Напомним, что NIL-узлы являются чёрными (по определению красно-чёрного дерева узел S может быть как красным, так и чёрным).
После удаления узла S образуются связи его родительского узла с NIL-узлом (узлами).
При этом, если узел S - красный, то чёрная высота дерева не изменится, и свойство красного узла будет также соблюдено:
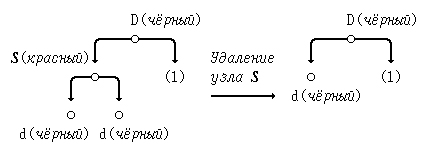
Если узел S - чёрный, то при его удалении количество чёрных узлов в пути до корневого узла уменьшится на 1. Исправление этой ситуации потребует анализа цветовой гаммы близлежащих узлов: "отца", "брата" и, возможно, "племянников" (см. случай (3)).
2. Узел S имеет один внутренний дочерний узел ("ребёнок") и один внешний дочерний узел (NIL-узел).
Удаление узла S приводит к образованию связи его родительского узла с его ребёнком.
При этом, если узел S - красный, то его удаление не приведёт к изменению чёрной высоты дерева и свойство красного узла будет также выполнятся, т.к. единственный реальный дочерний узел узла S может быть только чёрным:
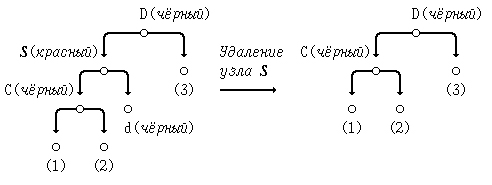
Если же узел S - чёрный, то его "ребёнок" C может быть как красным, так и чёрным.
Если же "ребёнок" C является красным, то при удалении его родителя S (чёрного узла) необходимо позаботиться о восполнении чёрных узлов рассматриваемой ветви дерева и, возможно, исправления нарушения свойства красного узла, если новый родительский узел оказался красным.
Выход из ситуации виден на приведённом ниже рисунке: требуется перекрасить красный дочерний узел С в чёрный цвет при перемещении его вверх для замещения удалённого узла S.
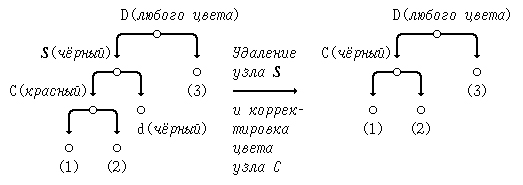
Более сложным является случай, когда "ребёнок" C - чёрный, тогда восполнение чёрной высоты дерева после удаления узла S будет невозможным за счёт узла C (см. случай (3)).
3. Узел S имеет два внутренних дочерних узла.
Удаление узла S подразумевает образование связи его родительского узла с его наследником, ключ которого является следующим по порядку (на множестве целых чисел) ключей вершин дерева.
Этот случай не отличается от двух рассмотренных, поскольку удаление узла S с двумя дочерними узлами сведётся к рассмотрению его наследника C как нарушающего свойства красно-чёрного дерева (назовём этот узел нарушающим узлом).
Таким образом, осталось решить две проблемы, отложенные в случаях (1) и (2): нарушение чёрной высоты при удалении чёрного узла, у которого либо нет "детей", либо есть "ребёнок" - чёрный узел, а родительский узел является чёрным.
Попытаемся свести оба случая к одному. Мы должны принять во внимание родительский и братский узлы нарушающего узла и два дочерних узла братского узла (узлы-племянники).
В данном случае можно считать, что братский узел не является внешним.
Это связано с соблюдением чёрной высоты бинарного дерева поиска: все пути, проходящие через удалённый и родительский узлы, имеют то же количество чёрных узлов, что и пути, проходящие через братский и родительский узлы.
Поскольку родительский узел чёрный, а удалённый узел и заменивший его дочерний узел также имеют чёрный цвет, то и все пути, проходящие через братский узел, должны содержать, по меньшей мере, два чёрных узла. Отсюда следует, что, как минимум, братский узел является чёрным и имеет два чёрных дочерних узла.
Продемонстрируем сказанное рисунком:
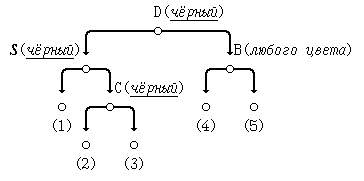
Если бы братский узел был красным, то его дочерние узлы должны были быть чёрными и, более того, чтобы свойство чёрного узла изначально выполнялось, то они должны были бы иметь собственные дочерние узлы.
Следовательно, это преобразование сохраняет существование братского узла с дочерними узлами и красно-чёрное состояние дерева.
(1)Бакнелл Д.М. Фундаментальные алгоритмы и структуры данных в Delphi. - СПб.: ООО "ДиаСофтЮП", 2003. - 560 с.
На следующем шаге мы рассмотрим корректировку свойств красно-чёрного дерева после удаления узла.
