На этом шаге мы рассмотрим структуру такой матрицы.

    Пусть G - помеченный граф порядка N, V={1, 2, ..., N}.

    Классическим способом представления неориентированного графа является матрица смежности - это матрица B ⇔ [B_ij] размера N × N, где

        ⌈ 1, если существует ребро, соединяющее вершины i и j;
   B ⇔ 
        ⌊ 0, в противном случае.
   

    Аналогично способом представления ориентированного графа является матрица смежности - это матрица B ⇔ [B_ij] размера N × N, где

        ⌈ 1, если существует дуга, соединяющее вершины i и j;
   B ⇔ 
        ⌊ 0, в противном случае.

    Основным достоинством представления графа с помощью матрицы смежности является тот факт, что за один шаг можно получить ответ на вопрос: "Существует ли ребро из вершины i в вершину j?".

    Основным недостатком является тот факт, что независимо от количества рёбер объём занятой памяти составляет N × N.

    На практике это неудобство можно уменьшить, сохраняя целую строку (столбец) матрицы в одном машинном слове (для малых N).

    Для представления матрицы смежности в виде S-выражения воспользуемся следующей структурой: строки матрицы определим как упорядоченные списки их элементов, а саму матрицу как список строк.

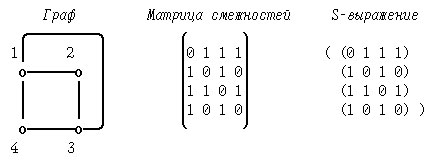
Рис.1. S-выражение, соответствующее неориентированному графу

    Построим S-выражение, соответствующее ориентированному графу:

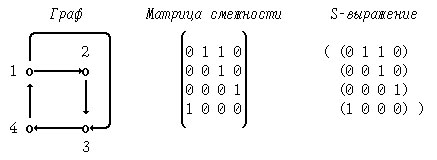
Рис.1. S-выражение, соответствующее ориентированному графу

    Представление графов с помощью матриц смежности иногда удобно в теоретических рассуждениях; например имеют место следующая теорема [1, с.28]: графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одинаковыми перестановками строк и столбцов.

    Рассмотренная в приведённой на следующем шаге программе реализация матрицы смежности с помощью S-выражения является неэффективной: основным её недостатком является отсутствие прямого доступа к элементам матрицы.

    На следующем шаге мы приведем демонстрационный пример.

Предыдущий шаг Содержание Следующий шаг