На этом шаге мы рассмотрим формирование такого списка и перечислим функции для работы с ним.
Опишем один из самых удобных способов представления графов на языке Haskell.
- Определение.
- Ассоциативным списком инцидентности будем называть способ моделирования списков инцидентности на языке Haskell, при котором списки инцидентности представлены в виде ассоциативного списка: первый элемент пары, входящей в этот список, представляет собой вершину графа, а второй элемент - это список вершин, смежных с данной.
Примеры ассоциативных списков инцидентности.
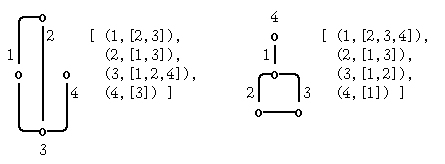
Рис.1. Ассоциативные списки инцидентности
Приведём основные функции библиотеки для работы с графами, представленными в виде ассоциативных списков инцидентности:
- (pairLis key data graph) - построение графа из списка вершин key и списка списков смежных вершин data с помощью добавления к существующему графу graph;
- (reKey graph) - восстановление списка вершин графа graph из ассоциативного списка инцидентности;
- (reData graph) - восстановление списка списков смежных вершин графа graph из ассоциативного списка инцидентности;
- (assoc1 node graph) - построение списка вершин графа graph, содержащего вершины, смежные вершине node;
- (rAssoc lst graph) - поиск в графе graph одной из вершин, имеющей заданный список смежных вершин lst;
- (putAssoc1 key data graph) - изменение в графе graph списка вершин, смежных вершине key, на список data;
- (addArc x y graph) - добавление в граф graph дуги (x,y);
- (deleteNode x graph) - удаление вершины x из графа graph;
- (deleteArc x y graph) - удаление дуги (x,y) из графа graph;
- (walk graph) - построение списка, содержащего все вершины графа, заданного ассоциативным списком инцидентности graph;
- (neighb2 x graph) - построение списка всех "соседей" данной вершины x в графе graph, представленном в виде ассоциативного списка инцидентности.
На следующем шаге мы рассмотрим пример использования перечисленных функций.
