На этом шаге мы рассмотрим реализацию этого алгоритма.

Рассмотрим теперь алгоритм обхода графа, известный под названием обход в ширину (поиск в ширину). При обходе графа в глубину, чем позднее будет посещена вершина, тем раньше она будет использована. Это прямое следствие того факта, что просмотренные, но ещё не использованные вершины накапливаются в стеке.

Обход графа в ширину основывается на замене стека очередью. После такой модификации, чем раньше посещается вершина (помещается в очередь), тем раньше она используется (удаляется из очереди). Использование вершины происходит с помощью просмотра сразу всех ещё непросмотренных вершин, смежных этой вершине. Таким образом, "поиск ведётся как бы во всех возможных направлениях одновременно" [1, с.131].

Механизм работы алгоритма обхода в ширину становится ясным из рассмотрения бинарного дерева поиска для следующего графа (порядок обхода графа задан цифрами рядом с кружками):

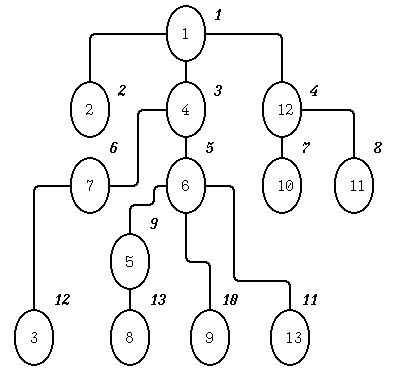
Рис.1. Пример дерева для обхода в ширину

Приведем программу, реализующую обход в ширину.

Раскрыть/скрыть текст примера.

   -- Демонстрация реализации алгоритма обхода графа 
   -- в ширину, начиная с указанной вершины
   -- [Крюков,Радионов,Таранов,Шаблыгин,1991,с.131]
   ------------------------------------------------
   import LibGrp_2
   ------------------------------------------------------
   -- Функция возвращает список вершин графа в порядке их
   -- прохождения в ширину;
   -- graph - граф в виде ассоциативного списка инцидентности,
   -- root - вершина графа, с которой начинается обход
   ----------------------------------------------------------------
   breadthFirst graph root = brfi graph [root] (neighb2 root graph)
   ----------------------------------------------------------------
   -- visited - список уже просмотренных вершин;
   -- queue - очередь вершин, ожидающих просмотра
   ----------------------------------------------
   brfi graph visited queue 
                 | null queue = reverse visited
                 | elem (head queue) visited 
                              = brfi graph visited (tail queue) 
                 | True       = brfi graph
                                     ((head queue):visited)
                                     (queue ++ neighb2 (head queue)
                                                       graph)
   ----------------------------------------------------------
   -- Неудачные тестовые примеры:
   ---------------------------------------------------------
   test =   breadthFirst [(1,[2,3,4]),(2,[1,3]),(3,[1,2,4]),
                          (4,[1,3,5]),(5,[4])] 4 == [4,1,3,5,2]
         && breadthFirst [(1,[2,3,4]),(2,[3]),(3,[4])] 1 
                                                 == [1,2,3,4]
         && breadthFirst [(1,[2,3,4]),(2,[3]),(3,[4])] 2 
                                                 == [2,3,4]
         && breadthFirst [(1,[2,3,4]),(2,[3]),(3,[4])] 3 
                                                 == [3,4]
         && breadthFirst [(1,[2,3,4]),(2,[3,1]),(3,[4])] 2 
                                                 == [2,3,1,4]
   ----------------------------------------------------------
   -- "Обход дерева поиска в ширину..."
   -------------------------------------------------------
         && breadthFirst [(1,[2,3]),(2,[4,5]),(3,[6,7])] 1 
                                     == [1,2,3,4,5,6,7]
         && breadthFirst [(10,[5,15]),(5,[3,7]),(7,[6,8]),
                          (15,[12,16]),(3,[]),(6,[]),(8,[]),
                          (12,[]),(16,[])] 10 
                                     == [10,5,15,3,7,12,16,6,8]
   ------------------------------------------------------------
   -- "'Обход' дерева поиска в ширину..."
   -------------------------------------------------------
         && breadthFirst [(10,[5,15]),(5,[3,7]),(7,[6,8]),
                          (15,[12,16])] 15 == [15,12,16]

Библиотека для работы с графами, представленными ассоциативными списками смежности.

Раскрыть/скрыть текст библиотеки.

   -- Библиотека для работы с графами, представленными ассо-
   -- циативными списками смежности.
   -- Ассоциативные списки смежности моделируются ассоциати-
   -- вным списком точечных пар следующего вида:
   --
   --   [(A ,[x ,x ,...,x ]),...,(A ,[y ,y ,...,y ])],
   --      1   1  2      k         n   1  2      j
   --
   -- каждая из которых описывает дугу, соединяющую вершины 
   --
   -- A  и x , A и x ,..., A  и x ,..., 
   --  1    1   1   2       1    k
   --
   -- A  и y , A  и y ,..., A  и y .
   --  n    1   n    2       n    j
   --
   -- Автор программы (на языке LISP): М.В.Швецкий 
   -- Переписано на язык Haskell: И.А.Кудрявцева (28.01.2010)
   ----------------------------------------------------------
   module LibGrp_2
      (pairLis,reKey,reData,assoc1,rAssoc,putAssoc1,addArc,
       deleteNode,deleteArc,walk,neighb2,oneRange,listSet,assoc)
   where
   import List
   -----------------------------------------------------------
   -- Построение графа  из  списка вершин KEY и списка списков
   -- смежных вершин DATA с помощью добавления к существующему
   -- графу Graph
   --------------------------------------------------------------
   pairLis:: [Integer] -> [[Integer]] -> [(Integer,[Integer])] ->
                                             [(Integer,[Integer])]
   pairLis key dta graph 
        | null key = graph
        | null dta = graph
        | elem (head key) (reKey graph)
                   = pairLis (tail key)
                             (tail dta)
                             (putAssoc1 (head key)
                                        (listSet
                                            (head dta ++
                                             (assoc1 (head key)
                                                     graph)))
                                        graph)
        | True     = (head key,head dta) :
                     pairLis (tail key) (tail dta) graph
   -----------------------------------------------------
   -- Восстановление списка вершин графа Graph из 
   -- ассоциативного списка инцидентности
   ------------------------------------------
   reKey:: [(Integer,[Integer])] -> [Integer]
   reKey graph | null graph = []
               | True       = fst (head graph) : reKey (tail graph)
   ----------------------------------------------------------------
   -- Восстановление списка списков смежных вершин графа
   -- Graph из ассоциативного списка инцидентности
   --------------------------------------------------
   reData:: [(Integer,[Integer])] -> [[Integer]]
   reData graph | null graph = []
                | True       = snd (head graph) : 
                               reData (tail graph)
   -----------------------------------------------------------
   -- Функция возвращает список вершин графа Graph, содержащий
   -- вершины, смежные вершине Node
   ------------------------------------------------------
   assoc1:: Integer -> [(Integer,[Integer])] -> [Integer]
   assoc1 node graph | null graph = []
                     | fst (head graph)==node
                                  = snd (head graph)
                     | True       = assoc1 node (tail graph)
   ------------------------------------------------------------
   -- Функция возвращает список из вершины графа Graph, имеющей 
   -- заданный список смежных вершин LST
   --------------------------------------------------------
   rAssoc:: [Integer] -> [(Integer,[Integer])] -> [Integer]
   rAssoc lst graph | null graph = []
                    | sort (snd (head graph))==sort lst
                                 = [fst (head graph)]
                    | True       = rAssoc lst (tail graph)
   ---------------------------------------------------------
   -- Изменение в графе Graph списка вершин, смежных вершине 
   -- Key, на список Data
   ------------------------------------------------------------
   putAssoc1:: Integer -> [Integer] -> [(Integer,[Integer])] -> 
                                              [(Integer,[Integer])]
   putAssoc1 key dta graph | null graph = []
                           | fst (head graph)/=key
                                        = head graph :
                                          putAssoc1 key dta 
                                                    (tail graph)
                           | True       = (fst (head graph),dta) :
                                          putAssoc1 key dta 
                                                    (tail graph)
   -------------------------------------------------------------
   -- Добавление в граф Graph дуги (x,y)
   -------------------------------------------------------
   addArc:: Integer -> Integer -> [(Integer,[Integer])] -> 
                                              [(Integer,[Integer])]
   addArc x y graph | null graph = [(x,[y])]
                    | fst (head graph)==x &&
                      not (elem y (snd (head graph)))
                                 = putAssoc1 x 
                                             (y : snd (head graph)) 
                                             graph 
                    | fst (head graph)==x &&
                      elem y (snd (head graph))
                                 = graph
                    | True       = head graph : addArc x y
                                                       (tail graph)
   ----------------------------------------------------------------
   -- Удаление вершины X из графа Graph
   ------------------------------------------------
   deleteNode:: Integer -> [(Integer,[Integer])] -> 
                                       [(Integer,[Integer])]
   deleteNode x graph 
        | (null graph) = []
        | fst (head graph)==x
                       = deleteNode x (tail graph)
        | elem x (snd (head graph)) 
                       = (fst (head graph),
                          filter (x/=) (snd (head graph))) :
                          deleteNode x (tail graph)
        | True         = head graph : deleteNode x (tail graph)
   ------------------------------------------------------------
   -- Удаление дуги (X,Y) из графа Graph
   ----------------------------------------------------------
   deleteArc:: Integer -> Integer -> [(Integer,[Integer])] -> 
                                              [(Integer,[Integer])]
   deleteArc x y graph 
        | null graph = []
        | fst (head graph)==x && 
          elem y (snd (head graph))
                     = (x,filter (y/=) (snd (head graph))) :
                          deleteArc x y (tail graph)
        | True       = head graph : deleteArc x y (tail graph)
   --------------------------------------------------------------
   -- Построение списка, содержащего все вершины графа, заданного
   -- ассоциативным списком инцидентности Graph
   --------------------------------------------
   walk:: [(Integer,[Integer])] -> [Integer]
   walk graph | null graph = []
              | True       = sort (listSet (oneRange graph))
   ---------------------------------------------------------
   -- Функция возвращает всех "соседей" данной вершины X 
   -- в графе Graph, представленном в виде ассоциативного 
   -- списка инцидентности
   -------------------------------------------------------
   neighb2:: Integer -> [(Integer,[Integer])] -> [Integer]
   neighb2 x graph | null (assoc x graph (==))
                          = []
                   | True = snd (head (assoc x graph (==)))
   --------------------------------------------------------
   -- Вспомогательные функции библиотеки:
   --------------------------------------
   -- Преобразование списочной структуры 
   --
   --  ((A .(x  x ... x ))...(A .(y  y ... y ))),
   --     1   1  2     k       n   1  2     j
   --
   -- в одноуровневый список
   ---------------------------------------------
   oneRange:: [(Integer,[Integer])] -> [Integer]
   oneRange lst | null lst = []
                | True     = (fst (head lst) : snd (head lst)) 
                             ++ oneRange (tail lst)
   -------------------------------------------------------
   -- Преобразование одноуровневого списка LST в множество 
   -- (удаление из списка повторяющихся элементов)
   -----------------------------------------------
   listSet:: [Integer] -> [Integer]
   listSet lst | null lst = []
               | elem (head lst) (tail lst)
                          = listSet (tail lst)
               | True     = head lst : listSet (tail lst)
   -------------------------------------------------------------
   -- Функция, выполняющая линейный поиск в ассоциативном списке
   -- alist пары, для которой при сравнении  её  fst-элемента  с
   -- ключом key по тесту test признак не равен False.  
   -- Если пара элементов,  удовлетворяющая  тесту, найдена,  то
   -- возвращается список из этой пары; иначе - пустой список
   ----------------------------------------------------------
   assoc:: Integer -> [(Integer,[Integer])] -> 
            (Integer -> Integer -> Bool) -> [(Integer,[Integer])]
   assoc key alist test | null alist = []
                        | test (fst (head alist)) key
                                     = [head alist]
                        | True       = assoc key (tail alist) test

Все файлы можно взять здесь.

При поиске в ширину ближайшие соседи последней просмотренной вершины добавляются в конец списка queue операцией:

   queue ++ (neighbour (head queue) graph),

в то время как новые вершины для просмотра берутся из начала этого списка, в который они помещаются с помощью операции

  (head queue): visited,

т.е. параметр queue представляет собой очередь в отличие от параметра path функции defi, который работает как стек. Это приводит к тому, что в процессе работы функции brfi просмотренные вершины в списке visited расположены в порядке невозрастания их расстояния от начальной вершины root.

⁽¹⁾Крюков А.П., Радионов А.Я., Таранов А.Ю., Шаблыгин Е.М. Программирование на языке R-Лисп. - М.: Радио и связь, 1991. - 192 с.

На следующем шаге мы рассмотрим нерекурсивный алгоритм поиска в ширину на графе.

Предыдущий шаг Содержание Следующий шаг