На этом шаге мы приведем иерархию классов и дадим краткую характеристику каждого класса.

Что такое "класс"?

Приведём иерархию классов, определённых в стандартном модуле Prelude.hs (по [1, с.183, 192-206]):

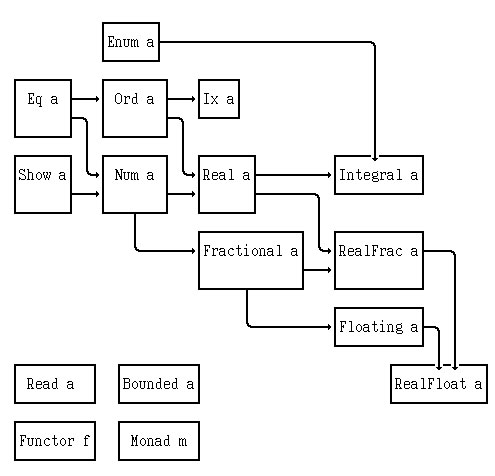
Рис.1. Иерархия классов

Класс Eq определяет класс типов, над которыми определены отношения равенства. Результат сравнения элементов таких типов представляет собой значение булевского типа (True - "истина", False - "ложь").
Операции класса Eq a:
```
   (==), (/=) :: a -> a -> Bool
```
Класс Show определяет шаблон для типов, элементы которых имеют графически представляемую форму. Все элементы таких типов можно передать в функцию show для вывода на экран (в консоль).
Операции класса Show a:
```
   show      :: a -> String
   showsPrec :: Int -> a -> ShowS
   showList  :: [a] -> ShowS
```
Значения из множеств-экземпляров класса Enum могут быть пронумерованы с помощью некоторого целого числа - уникального для конкретного значения типа.
Таким образом, может быть определён порядок следования элементов такого типа.
Операции класса Enum a:
```
   succ, pred     :: a -> a
   toEnum         :: Int -> a
   fromEnum       :: a -> Int
   enumFrom       :: a -> [a]              -- [n..]
   enumFromThen   :: a -> a -> [a]         -- [n,m..]
   enumFromTo     :: a -> a -> [a]         -- [n..m]
   enumFromThenTo :: a -> a -> a -> [a]    -- [n,n'..m]
```
Класс Ord определяет шаблон для типов, над экземплярами которых определён порядок следования.
Операции класса Ord a:
```
   compare              :: a -> a -> Ordering
   (<), (<=), (>=), (>) :: a -> a -> Bool
   max, min             :: a -> a -> a
```
Здесь
```
   Ordering ↔ {EQ,LT,GT},
```
где EQ - "равно", LT - "меньше или равно", GT - "больше".
Класс Num является родительским для всех числовых классов. Любой экземпляр этого класса должен поддерживать элементарные арифметические операции (сложение, вычитание и умножение).
Операции класса Num a:
```
   (+), (-), (*) :: a -> a -> a
   negate        :: a -> a
   abs, signum   :: a -> a
   fromInteger   :: Integer -> a
   fromInt       :: Int -> a
```
Класс Ix определяет шаблон для типов, значения которых могут выступать в качестве индексов в массивах данных.
Операции класса Ix a:
```
   range              :: (a,a) -> [a]
   index, unsafeIndex :: (a,a) -> a -> Int
   inRange            :: (a,a) -> a -> Bool
   rangeSize          :: (a,a) -> Int
```
Класс Real определяет класс числовых типов, элементы которых могут быть представлены как отношения (например, рациональные числа).
Операции класса Real a:
```
   toRational :: a -> Rational
```
Класс Fractional определяет шаблон для любого типа, элементами которого являются дробные (рациональные) числа.
    Все такие типы должны иметь определённую операцию деления.
    Кроме того, каждый элемент должен иметь обратное значение относительно операции деления.
    Далее, все значения этого класса должны иметь возможность преобразования из рациональных чисел.
    Операции класса Fractional a:
```
   (/)          :: a -> a -> a
   recip        :: a -> a
   fromRational :: Rational -> a
   fromDouble   :: Double -> a
```
Класс Integral определяет шаблон для любого типа, который содержит в себе любые целые числовые элементы.
Операции класса Intgral a:
```
   quot, rem, div, mod :: a -> a -> a
   quotRem, divMod     :: a -> a -> (a,a)
   toInteger           :: a -> Integer
   toInt               :: a -> Int
```
Класс RealFrac объединяет в себе свойства классов Real и Fractional, но при этом дополнительно включающий некоторые функции для работы с числами, представленными в виде значений с плавающей точкой, а именно функции для округления величин.
Операции класса RealFrac a:
```
   properFraction  :: (Integral b) => a -> (b,a)
   truncate, round :: (Integral b) => a -> b
   ceiling, floor  :: (Integral b) => a -> b
```

Класс Floating определяет поведение всех числовых типов, чьи элементы являются числами с плавающей точкой.

Операции класса Floating a:

   pi                  :: a
   exp, log, sqrt      :: a -> a
   (**), logBase       :: a -> a -> a
   sin, cos, tan       :: a -> a
   asin, acos, atan    :: a -> a
   sinh, cosh, tanh    :: a -> a
   asinh, acosh, atanh :: a -> a

Класс RealFloat объединяет в себе свойства классов RealFrac и Floating, но при этом дополнительно описывающий некоторые функции для работы с числами, представленными в виде значений с плавающей точкой.

Операции класса RealFloat a:

   floatRadix       :: a -> Integer
   floatDigits      :: a -> Int
   floatRange       :: a -> (Int,Int)
   decodeFloat      :: a -> (Integer,Int)
   encodeFloat      :: Integer -> Int -> a
   exponent         :: a -> Int
   significand      :: a -> a
   scaleFloat       :: Int -> a -> a
   isNaN, isInfinite, isDenormalized, isNegativeZero, isIEEE
                    :: a -> Bool
   atan2            :: a -> a -> a

Класс Read представляет шаблон для типов, элементы которых имеют строковое представление.
Операции класса Read a:
```
   readsPrec :: Int -> ReadS a
   readList  :: ReadS [a]
```
Экземпляры класса Bounded представляют собой множества, ограниченные сверху и снизу. Это означает, что имеются минимальный элемент множества и максимальный элемент множества.
Однако само множество вполне может быть и неупорядоченным - в нём может отсутствовать отношение порядка.
Операции класса Bounded a:
```
   minBound, maxBound :: a
```

⁽¹⁾Душкин Р.В. Функциональное программирование на языке Haskell. - М.: ДМК Пресс, 2007. - 608 с.

На следующем шаге мы рассмотрим создание экземпляров классов.

Предыдущий шаг Содержание Следующий шаг