На этом шаге мы рассмотрим решение матричных игр методами линейного программирования.
Теория игр находится в тесной связи с линейным программированием, так как любую конечную игру двух лиц с нулевой суммой можно представить в виде задачи линейного программирования и наоборот. Дж. Данциг отмечает, что, когда в 1947 году создатель теории игр Дж. фон Нейман впервые ознакомился с симплекс-методом, он сразу установил эту взаимосвязь и обратил особое внимание на концепцию двойственности в линейном программировании. Этот шаг иллюстрирует решение матричных игр методами линейного программирования.
Оптимальные значения вероятностей xi, i = 1, 2, ..., m, игрока А могут быть определены путем решения следующей максиминной задачи.
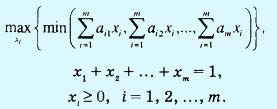
Чтобы сформулировать эту задачу в виде задачи линейного программирования, положим
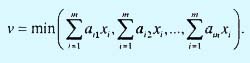
Отсюда вытекает, что
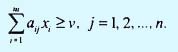
Следовательно, задача игрока А может быть записана в виде
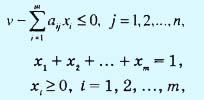
Отметим последнее условие, что цена игры v может быть как положительной, так и отрицательной. Оптимальные стратегии y1, y2, ...,yn игрока В определяются путем решения задачи
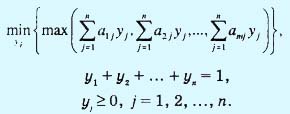
Используя процедуру, аналогичную приведенной выше для игрока А, приходим к выводу, что задача для игрока В сводится к следующему.
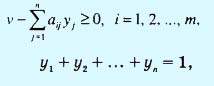
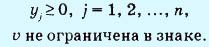
Две полученные задачи оптимизируют одну и ту же (не ограниченную в знаке) переменную v, которая является ценой игры. Причиной этого служит то, что задача игрока В является двойственной к задаче игрока А. Это означает, что оптимальное решение одной из задач автоматически определяет оптимальное решение другой.
На следующем шаге рассмотрим пример решения матричной игры методами линейного программирования.
