На этом шаге будем проводить анализ модели на чувствительность к изменению значений коэффициентов целевой функции.
В общем виде целевую функцию задачи ЛП с двумя переменными можно записать следующим образом: z = с1x1 + с2х2
Изменение значений коэффициентов c1 и c2 приводит к изменению угла наклона прямой z. Графический способ решения задачи ЛП показывает, что это может привести к изменению оптимального решения: оно будет достигаться в другой угловой точке пространства решений. Вместе с тем, очевидно, существуют интервалы изменения коэффициентов c1 и c2, когда текущее оптимальное решение сохраняется.
Задача анализа чувствительности и состоит в получении такой информации. В частности, представляет интерес определение интервала оптимальности для отношения c1/c2 (или, что то же самое, для c2/c1); если значение отношения c1/c2 не выходит за пределы этого интервала, то оптимальное решение в данной модели сохраняется неизменным.
Следующий пример показывает, как можно получить необходимый результат с помощью анализа графического представления модели ЛП.
Пример 1. Применим процедуру анализа чувствительности к модели для компании "Русские краски". На рис. 1 видно, что функция z = 5х1 + 4х2 достигает максимального значения в угловой точке С.
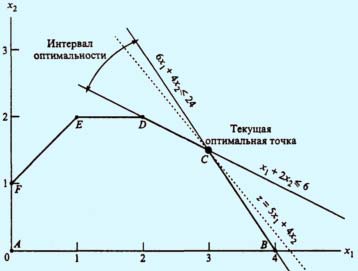
Рис. 1. Анализ чувствительности
При изменении коэффициентов целевой функции z = с1x1 + с2х2 точка С останется точкой оптимального решения до тех пор, пока угол наклона линии z будет лежать между углами наклона двух прямых, пересечением которых является точка С. Этими прямыми являются 6х1 + 4х2 = 24 (ограничение на сырье Ml) и х1 + 2х2 = 6 (ограничение на сырье М2).
Алгебраически это можно записать следующим образом:
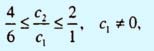 или
или 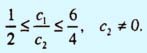
В первой системе неравенств условие c1 <> 0 означает, что прямая, соответствующая целевой функции, не может быть горизонтальной.
Аналогичное условие в следующей системе неравенств означает, что эта же прямая не может быть вертикальной.
Из рис. 1 видно, что интервал оптимальности данной задачи (он определяется двумя прямыми, пересекающимися в точке С) не разрешает целевой функции быть ни горизонтальной, ни вертикальной прямой. Таким образом, мы получили две системы неравенств, определяющих интервал оптимальности в нашем примере. (Когда c1 и c2 могут принимать нулевые значения, интервал оптимальности для отношения c1/c2 (или c2/c1 ) необходимо разбить на два множества, где знаменатели не обращались бы в нуль.
Итак, если коэффициенты c1 и c2 удовлетворяют приведенным выше неравенствам, оптимальное решение будет достигаться в точке С.
Отметим, если прямая z = с1x1 + с2х2 совпадет с прямой х1 + 2х2 = 6, то оптимальным решением будет любая точка отрезка CD.
Аналогично, если прямая, соответствующая целевой функции, совпадет с прямой 6x1 + 4х2 = 24, тогда любая точка отрезка ВС будет оптимальным решением. Однако заметим, что в обоих случаях точка С остается точкой оптимального решения.
Приведенные выше неравенства можно использовать при определении интервала оптимальности для какого-либо одного коэффициента целевой функции, если предположить, что другой коэффициент остается неизменным. Например, если в нашей модели зафиксировано значение коэффициента с2 (пусть с2 = 4), тогда интервал оптимальности для коэффициента с1 получаем из неравенств 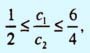 путем подстановки туда значения с2 = 4. После выполнения элементарных арифметических операций получаем неравенства для коэффициента с1: 2 ≤ с1 ≤ 6.
путем подстановки туда значения с2 = 4. После выполнения элементарных арифметических операций получаем неравенства для коэффициента с1: 2 ≤ с1 ≤ 6.
Аналогично, если зафиксировать значение коэффициента с1 (например, с1 = 5), тогда из неравенств 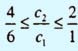 получаем интервал оптимальности для коэффициента с2: 10/3 ≤ с2 ≤ 10.
получаем интервал оптимальности для коэффициента с2: 10/3 ≤ с2 ≤ 10.
На следующем шаге рассмотрим расчет стоимости сырья - еще один способ анализа модели на чувствительность.
