На этом шаге рассмотрим пример применения симплекс-метода для решения задачи ЛП.
Используем задачу о компании "Русские краски" для рассмотрения деталей выполнения симплекс-метода.
Переменные задачи:
x1 - объем ежедневного производства краски для наружных работ (тонны),
x2 - объем ежедневного производства краски для внутренних работ (тонны).
Краска обоих видов производится из сырья M1 и М2. Первые два ограничения задачи порождены ограниченными ежедневными запасами сырья. Другие два отображают ограниченный рыночный спрос на краску. Прибыль от одной тонны краски для наружных работ составляет 5000 д.е., а краски для внутренних работ — 4000 д.е. Целевая функция задачи должна максимизировать общую прибыль. Для удобства вычислений доходность производства красок масштабирована в тысячах д.е.
Эта задача в стандартной форме записывается так:
Максимизировать z = 5x1 + 4x2 + 0sx3 + 0sx4 + 0sx5 + 0sx6
при ограничениях
6x1 + 4x2 + sx3 = 24 (Ограничение на сырье М1)
x1 + 2x2 + sx4 = 6 (Ограничение на сырье М2)
-x1 + 2x2 + sx5 = 1 (Ограничение на спрос)
x2 + sx6 = 2 (Ограничение на спрос)
x1, x2, sx3, sx4, sx5, sx6 ≥ 0.
Здесь sx3, sx4, sx5, sx6 — дополнительные (остаточные) переменные, добавленные в неравенства для преобразования их в равенства.
Задачу линейного программирования в стандартной форме можно представить в виде следующей таблицы:
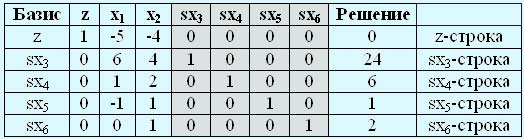
Нижние четыре строки этой таблицы представляют равенства ограничений; значения правых частей этих равенств даны в столбце "Решение". Строка z получена из равенства z - 5x1 - 4x2 = 0.
Дополнительные переменные sx3, sx4, sx5, sx6 составляют очевидное начальное допустимое базисное решение, при этом, поскольку небазисные переменные х1 и х2 равны нулю, их значения автоматически отображаются в столбце "Решение": sx3 = 24, sx4 = 6, sx5 = 1, sx6 = 2. Значение целевой функции при этом решении равно нулю.
Это решение не является оптимальным, поскольку переменные х1 и х2 здесь равны нулю, а возрастание этих переменных даже на единицу приводит к увеличению значения целевой функции z = 5x1 + 4x2 на 5 (при увеличении х1) или 4 единицы (при увеличении х2). Поскольку коэффициент при переменной х1, в формуле целевой функции больше, чем коэффициент при х2, переменную х1 следует ввести в число базисных (в этом случае она станет вводимой). Если обратиться к приведенной таблице, то вводимая переменная определяется среди множества небазисных как переменная, имеющая наибольший отрицательный коэффициент в z-строке.
Включаемая переменная х1 должна принять положительное значение. На рис. 1 видно, что, исходя из начальной точки A (x1 = 0, х2 = 0), наибольшее значение, которое можно присвоить переменной х1 (не выходя из пространства допустимых решений), равно 4, что соответствует точке В (х1 = 4, х2 = 0). Это означает, что решение переместилось от крайней точки А в крайнюю точку В.
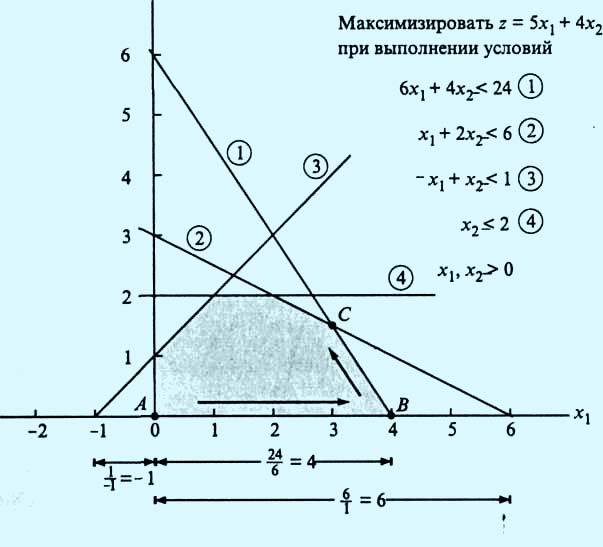
Рис. 1. Графическая интерпретация итерации симплекс-метода
Поскольку симплекс-метод не должен основываться на графическом представлении задачи линейного программирования, необходимо определить, как выбрать точку В алгебраически. Из рис. 1 видно, что В является одной из точек пересечения прямых, соответствующих ограничениям, с осью х1. Алгебраически точку пересечения можно найти как отношение правой части равенства (значение в столбце "Решение") к коэффициенту при переменной х1 в этом равенстве, как показано в следующей таблице:
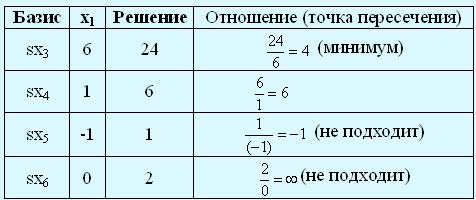
Нас интересуют только неотрицательные отношения (или точки пересечения на положительной полуоси x1), так как они соответствуют направлению возрастания переменной х1. Отметим, что все значения в столбце "Решение" неотрицательные, поэтому вычисляемое отношение будет неотрицательным и конечным только в том случае, если знаменатель отношения строго положителен.
Минимальное неотрицательное отношение равно значению вводимой переменной x1 в новом решении, а именно x1 = 4 (сравните с точкой В на рис. 1). Значение целевой функции при этом значении х1, возрастет до 20 (= 5 * 4).
Теперь среди текущих базисных переменных sx3, sx4, sx5, sx6 следует определить исключаемую переменную, которая примет нулевое значение после введения в базис переменной х1. Поскольку наименьшее (неотрицательное) отношение соответствует переменной sx3, в точке В именно эта переменная обращается в нуль. Таким образом, переменная sx3 будет исключаемой, в этом случае переменная х1 автоматически получает значение 4. Замена исключаемой переменной sx3 на вводимую переменную x1 приводит к новому базисному решению (x1, sx4, sx5, sx6).
Вычисление нового базисного решения основывается на методе исключения переменных (методе Гаусса-Жордана). В следующей таблице, которая пока совпадает с начальной таблицей задачи линейного программирования, определим ведущий столбец, ассоциируемый с вводимой переменной, и ведущую строку, ассоциируемую с исключаемой переменной. Элемент, находящийся на пересечении ведущего столбца и ведущей строки, назовем ведущим.
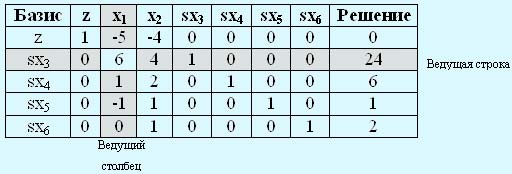
Процесс вычисления нового базисного решения состоит из двух этапов.
1. Вычисление элементов новой ведущей строки.
Новая ведущая строка = Текущая ведущая строка / Ведущий элемент.
2. Вычисление элементов остальных строк, включая z-строку.
Новая строка = Текущая строка - Ее коэффициент в ведущем столбце * Новая ведущая строка.
В нашем примере ведущая строка (sx3-строка) делится на ведущий элемент (= 6). В следующей таблице показана новая ведущая строка, где вводимая (небазисная) переменная х1 заменила исключаемую переменную sx3. В столбце "Решение" получаем новое значение переменной х1 (= 4).
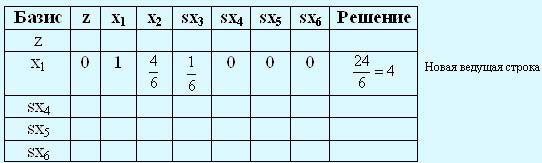
Вычисляем элементы остальных строк таблицы:
1. z-строка:

2. sx4-строка:

3. sx5-строка:

4. sx6-строка повторяет текущую sx6-строку, т.к. ее коэффициент в ведущем столбце равен нулю.
Новая симплекс-таблица, соответствующая новому базисному решению имеет вид:
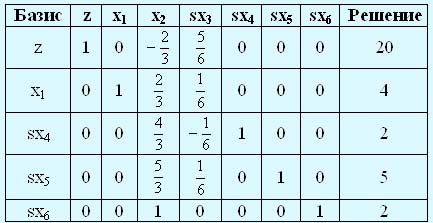
Отметим, что новая таблица обладает теми же свойствами, что и начальная: только небазисные переменные х2 и sx3 равны нулю, в столбце "Решение" представлено новое базисное решение (х1 = 4, sx4 = 2, sx5 = 5, sx6 = 2) вместе с новым значением целевой функции z (= 20). Это результат применения метода Гаусса-Жордана.
Из последней таблицы видно, что полученное базисное решение не является оптимальным, поскольку в z-строке переменная х2 имеет отрицательный коэффициент. Так же, как и в начальной таблице, строку z можно интерпретировать как уравнение z = 2/3x2 - 5/6sx3 + 20.
Из последнего уравнения следует, что увеличение значения переменной х2 (ее текущее значение равно нулю) приведет к увеличению значения целевой функции. Таким образом, переменная х2 должна стать вводимой в базис.
Далее определим исключаемую переменную. Для этого вычислим отношения правых частей равенств, соответствующих ограничениям, к коэффициентам, стоящим при х2 в этих равенствах.
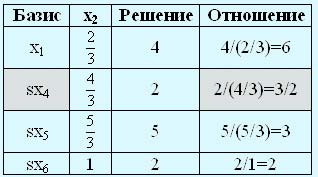
Вычисления показывают, что минимальное (неотрицательное) отношение соответствует переменной sx4, которая становится исключаемой; при этом значение отношения (= 3/2) равно новому значению переменной х2.
Соответствующее увеличение значения целевой функции составит 2/3*3/2 = 1 и z = 20 + 1 =21. В этой ситуации ведущей строкой будет sx4-строка, а ведущим столбцом — столбец, соответствующий переменной х2. Ведущий элемент равен 4/3.
Вычисляем элементы новой симплекс-таблицы.
1. Новая ведущая (sx4-) строка = Текущая sx4-строка / 4/3.
2. Новая строка z-строка = Текущая z-строка - (-2/3) * Новая ведущая строка.
3. Новая x1-строка = Текущая x1-строка – 2/3 * Новая ведущая строка.
4. Новая sx5-строка = Текущая sx5-строка – 5/3 * Новая ведущая строка.
5. Новая sx6-строка = Текущая sx6-строка - 1 * Новая ведущая строка.
Эти вычисления приводят к следующей таблице.
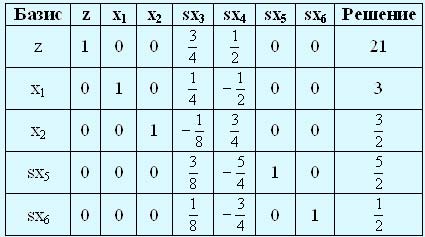
Поскольку z-строка не имеет отрицательных коэффициентов, соответствующих небазисным переменным sx3 и sx4, полученное решение оптимально.
Оптимальное решение задачи линейного программирования можно "считать" из симплекс-таблицы следующим образом. Неотрицательные (базисные) переменные представлены в столбце "Базис", а их значения — в столбце "Решение". В данном примере имеем следующее:
- ежедневно следует производить 3 т краски для наружных работ;
- ежедневно следует производить 1,5 т краски для внутренних работ;
- ежедневный доход составляет 21000 д.е.
С помощью симплекс-таблицы можно получить много дополнительной информации (кроме непосредственно оптимального решения).
1. Состояние ресурсов.
2. Цена единицы ресурсов (двойственные цены).
3. Все данные, необходимые для проведения анализа чувствительности оптимального решения.
Покажем, как определить состояние (статус) ресурсов. Статус ресурса определяется как дефицитный или недефицитный, в зависимости от того, будет он использован полностью или нет. Эту информацию можно получить из результирующей симплекс-таблицы путем проверки значений дополнительных (остаточных) переменных, ассоциируемых с соответствующими ограничениями, накладываемыми на ресурсы.
Если дополнительная переменная равна нулю, значит, ресурс использован полностью, и он получает статус дефицитного.
Положительное значение дополнительной переменной указывает на недефицитность соответствующего ресурса.
В задаче о компании "Русские краски" четыре ограничения классифицируются следующим образом.

Статус ресурсов показывает, что, поскольку M1 и М2 дефицитны, их увеличение может привести к улучшению оптимального решения (т.е. увеличению значения целевой функции).
На следующем шаге рассмотрим применение программы TORA для решения задачи линейного программирования симплекс-методом.
