Шаг 39.
Определение двойственной задачи

    На этом шаге рассмотрим определение двойственной задачи.

    Исходную задачу линейного программирования будем называть прямой. Двойственная задача — это задача, формулируемая с помощью определенных правил непосредственно из прямой задачи.

    При изложении теории двойственности часто рассматривают формулировки двойственной задачи в зависимости от различных видов прямой задачи, которые определяются типами ограничений, знаками переменных (неотрицательные или свободные, т.е. без ограничения в знаке) и типом оптимизации (максимизация или минимизация целевой функции). Приведем единую формулировку двойственной задачи, применимую ко всем видам прямой задачи. В основу такой формулировки положена стандартная форма прямой задачи. Напомним, что задача ЛП в стандартной форме записывается следующим образом. Максимизировать или минимизировать целевую функцию

при ограничениях

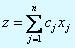
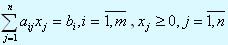
    В состав n переменных х_j входят также дополнительные переменные. Стандартная форма задачи линейного программирования предполагает выполнение следующих условий.

1. Все ограничения записаны в виде равенств (с неотрицательной правой частью).
2. Все переменные неотрицательны.
3. Оптимизация определяется как максимизация или минимизация целевой функции.

    Стандартная форма задачи линейного программирования порождает стандартную таблицу симплекс-метода. Решение двойственной задачи можно получить непосредственно из симплекс-таблицы, соответствующей оптимальному решению прямой задачи. Таким образом, определив двойственную задачу на основе стандартной формы прямой задачи, после вычислений симплекс-метода мы автоматически получаем решение двойственной задачи. Переменные и ограничения двойственной задачи формируются путем симметричных структурных преобразований прямой задачи по следующим правилам:

1. Каждому из m ограничений прямой задачи соответствует переменная двойственной задачи.
2. Каждой из n переменных прямой задачи соответствует ограничение двойственной задачи.
3. Коэффициенты при какой-либо переменной в ограничениях прямой задачи становятся коэффициентами ограничения двойственной задачи, соответствующей этой переменной, а правая часть формируемого ограничения равна коэффициенту при этой переменной в выражении целевой функции.
4. Коэффициенты целевой функции двойственной задачи равны правым частям ограничений прямой задачи.

    Графически эти правила можно представить:

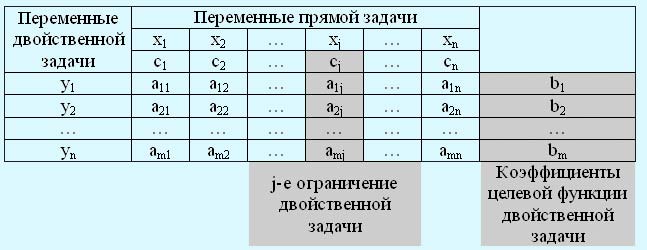
    Правило определения типа оптимизации, ограничений и знака переменных двойственной задачи:

    На следующм шаге рассмотрим пример на построение двойственной задачи из прямой задачи.

Предыдущий шаг Содержание Следующий шаг