На этом шаге мы рассмотрим функцию filter().
Вторая категория функций в функциональном программировании - это фильтры. Фильтр принимает функцию предиката, которая проверяет каждый элемент на соответствие условию и возвращает истину или ложь. Если предикат возвращает истину, то элемент будет добавлен в новую коллекцию, созданную фильтром. Если предикат возвращает ложь, то элемент не войдет в новую коллекцию.
Один из фильтров имеет соответствующее название filter(). Начнем с примера объединения filter() с flatMap(). Введите следующий код в REPL.
val itemsOfManyColors = listOf(listOf("red apple", "green apple", "blue apple"), listOf("red fish", "blue fish"), listOf("yellow banana", "teal banana")) val redItems = itemsOfManyColors.flatMap { it.filter { it.contains("red") } } print(redltems) [red apple, red fish]
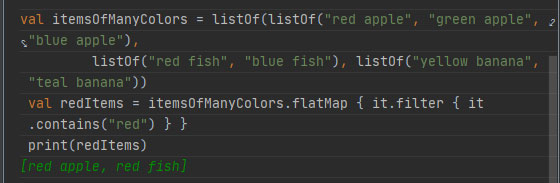
Рис.1. Фильтрация и объединение (REPL)
В этом примере flatMap() принимает преобразователь filter(), позволяя вам обработать каждый подсписок до их объединения.
Преобразователь filter(), в свою очередь, принимает функцию-предикат с условием для проверки:
{ it.contains("red") } .
В конце flatMap() объединяет элементы из подсписков, получившихся в результате преобразования, в новый единый список.
Цепочка функций - это основа функционального программирования. Введите следующий пример в Kotlin REPL.
val numbers = listOf(7, 4, 8, 4, 3, 22, 18, 11) val primes = numbers.filter { number -> (2 until number).map { number % it } .none { it == 0 } } print(primes) [7, 3, 11]
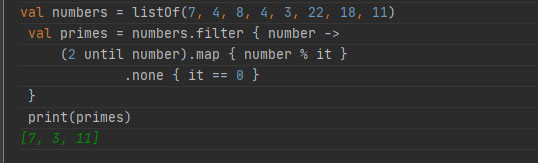
Рис.2. Фильтрация непростых чисел (REPL)
Вы реализовали решение довольно сложной задачи с помощью нескольких простых функций. Это фирменный стиль функционального программирования: небольшие операции, которые выполняют работу совместно для получения итогового результата.
Значение, возвращаемое предикатом в функции fliter() в этом примере, является результатом работы другой функции - map(). Каждое число в numbers map() делится на каждое значение в интервале от 2 до этого числа и возвращает список с остатками от деления. Далее, none возвращает истину, если ни один из остатков не равен 0. Если это так, значит, условие выполняется и проверяемое число является простым (простые числа - это числа, которые без остатка делятся только на 1 и на самого себя).
На следующем шаге мы рассмотрим комбинаторы.
