На этом шаге мы начинаем рассматривать функции пользователя. В частности,
поговорим о функции LAMBDA.
В результате почти полувековой практики программирования был разработан весьма эффективный способ составления программ, при котором задача разбивается на подзадачи, а те, в свою очередь, дробятся на элементарные функции, определенное сочетание которых реализует решение подзадач и соответственно всей задачи. Процесс дробления на элементарные функции заканчивается тогда, когда каждая из полученных функций выполняет некоторую логически отдельную операцию и результат работы данной функции может служить входом для другой функции. Такое разбиение приводит к тому, что задача представляется некоторым минимальным набором функций, который и кодируется на языке, адекватном характеру задачи.
Проблема выбора подфункций при разработке основной функции является извечной проблемой хорошего структурирования программы. Иногда стандартные подфункции выявляются сами собой, но более часты случаи, когда удачный подбор подфункций специального назначения может значительно упростить структуру множества функций в целом.
Вычисляемые функции.
Определение функций и их вычисление в языке LISP основано на лямбда-исчислении Черча. Лямбда-выражение, позаимственное языком из лямбда-исчисления является важным механизмом в практическом программировании.
В лямбда-исчислении Черча функция записывается в следующем виде:
lambda (x1,x2,...,xN).fN .
В языке LISP лямбда-выражение имеет вид:
(LAMBDA (X1 X2 ... XN) FN)
Функция LAMBDA предназначена для определения "безымянных" функций и называется вычисляемой функцией (не путать с понятием вычислимой функции в теории алгоритмов!).
Первый аргумент вычисляемой функции - (X1 X2 ... XN) является списком (возможно, пустым!). Его называют лямбда-списком. X1, X2,...,XN называются формальными параметрами.
Формальность параметров означает, что их можно заменить на любые другие символы, и это не отразится на вычислениях, определяемых функцией. Именно это и скрывается за лямбда-нотацией.
Второй аргумент функции LAMBDA - FN называется телом. Оно представляет собой произвольное выражение, значение которого может вычислить интерпретатор языка LISP. Таким образом:
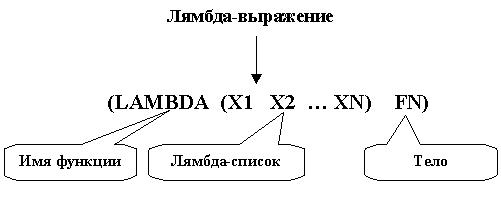
Рис.1. Вид лямбда-выражения
Для того, чтобы применить лямбда-функцию к аргументам, нужно в вызове функции
поставить лямбда-выражение вместо имени функции:
( (LAMBDA (X1 X2 ... XN) FN) A1 A2 ... AN)
Здесь Ai (i=1,2,...,N) - выражения языка LISP, определяющие фактические параметры. Такую форму вызова называют лямбда-вызовом.
Вычисление лямбда-вызова (применение лямбда-выражения к фактическим параметрам) производится в два этапа. Сначала вычисляются значения фактических параметров и соответствующие формальные параметры связываются с полученными значениями. Этот этап называется связыванием параметров.
На следующем этапе с учетом новых связей вычисляется тело лямбда-выражения, и полученное значение возвращается в качестве значения лямбда-вызова. Формальным параметрам после окончания вычисления возвращаются те связи, которые у них были перед вычислением лямбда-вызова.
Весь этот процесс называют лямбда-преобразованием (лямбда-конверсией).
Приведем несколько примеров лямбда-преобразований:
$ ((LAMBDA (NUM) (PLUS NUM 1)) 45)
46
$ ((LAMBDA (M N) (COND ((LESSP M N) M) (T N))) 233 123)
23
$ (LAMBDA NIL (PLUS 3 5))
8
$ (LAMBDA () (PLUS 3 5))
8
$ ((LAMBDA (X) (EQ X NIL)) NIL)
T
Лямбда-выражение - это "безымянная" функция, которая пропадает тотчас же после лямбда-преобразования. Ее трудно использовать снова, так как нельзя вызвать по имени, хотя лямбда-вызов доступен как списочный объект.
"Безымянные" функции используются, например, при передаче функции в качестве аргумента
другой функции или при формировании функции в результате вычислений, другими словами,
при синтезе программ.
На следующем шаге мы поговорим о невычисляемых функциях пользователя.
