На этом шаге мы рассмотрим функции, эквивалентные операторам присваивания в императивных языках программирования.

Операция присваивания при программировании на языке LISP не играет такой важной роли, как в языках императивного программирования. Многие LISP-программы написаны без единой операции присваивания; тот же эффект достигается косвенно, при помощи рекурсии и передачи параметров.

Различают глобальные и локальные значения атомов.

Локальные значения связываются с атомом лишь на время выполнения некоторых функций. Глобальные значения атомов могут быть установлены с помощью так называемых функций назначения SET и SETQ. Тогда, если атом, имеющий глобальное значение, выступает в качестве формального параметра какой-либо функции, то при лямбда-преобразовании он связывается с новым значением. После этого атому возвращается прежнее глобальное значение.

Функция SET связывает значение аргумента X с вычисленным значением S-выражения. Синтаксис функции:

        (SET X Y) ,

где X - атом, Y - S-выражение.

Например:

   $ (SET 'FOO '(A B C))    $ (SET 'PET 'DOG)
   (A B C)                  DOG
   $ FOO                    $ (SET PET 'ROVER)
   (A B C)                  ROVER
                            $ DOG
                            ROVER
                            $ PET
                            DOG

Заметим, что (SET X Y) эквивалентно X := Y в языках императивного программирования.

Обратите внимание на то, что функция SET вычисляет значения обоих аргументов, т.е. с ее помощью можно связать значение Y с именем, которое получается также путем вычисления. Например:

   $ (SET (CAR '(A B C)) 25)
   25
   $ A
   25

Связать символ с его значением можно и с помощью функции SETQ. Эта функция отличается от функции SET тем, что она вычисляет только свой второй аргумент. Об автоматическом блокировании вычисления первого аргумента напоминает буква Q (Quote) в имени функции.

Таким образом, (SETQ A B) эквивалентно (SET (QUOTE A) B).

Замечание. В реализации InterLISP есть функция SETQQ, которая блокирует вычисление обоих аргументов.

Пример 1. Генерация случайных целых чисел, не больших 8.

(DEFUN RANDOM (LAMBDA (SEED)
      (SETQ SEED (MOD
                     (+ 2113233
                           (* SEED 271821)) 9999991))
      (MOD SEED 8)
))

Текст этой функции можно взять здесь.

Функции SET и SETQ обладают еще и побочным эффектом. Эффект функции состоит в образовании связи между атомом и его значением. Атом остается связанным с определенным значением до тех пор, пока это значение не изменят.

Напомним, что функции, обладающие побочным эффектом, в языке LISP называют псевдофункциями. Мы будем все же как для функций, так и для псевдофункций использовать понятие функции, если только нет особой надобности подчеркнуть наличие побочного эффекта.

Графически будем изображать результат действия функции (SETQ SPISOK '(A B C)) следующим образом:

Рис.1. Иллюстрация определения списка

Пример 2. Допустим, что мы построили два списка:

   $ (SETQ GOLOWA '(B C))
   (B C)
   $ (SETQ HVOST '(A B C))
   (A B C)

Создадим новый список:

   $ (SETQ RES (CONS GOLOWA HVOST))
   ((B C) A B C)
   $ RES
   ((B C) A B C)

Изобразим результат построения на рисунке:

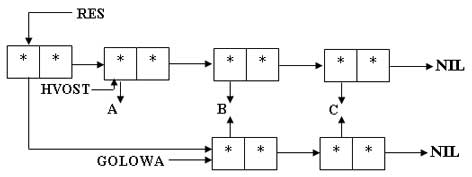
Рис.2. Результат построения

Нетрудно видеть, что на одну ячейку может указывать одна или более стрелок из списочных ячеек, однако из каждого поля ячейки может исходить лишь одна стрелка. Если на некоторую ячейку есть несколько указателей, то эта ячейка будет определять общее подвыражение.

В зависимости от способа построения логическая и физическая структуры двух списков могут оказаться различными.

Пример 3.

   $ (SETQ SPISOK1 '((B C) A B C))
   ((B C) A B C)

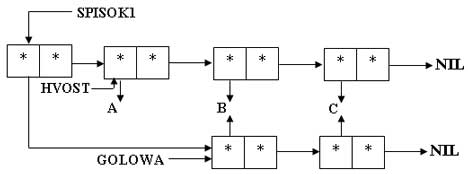
Рис.3. Определение списка SPISOK1

   $ (CAR SPISOK1)
   (B C)
   $ (CDDR SPISOK1)
   (B C)

Получены логически одинаковые списки.

   $ (SETQ BC '(B C))    
   (B C)

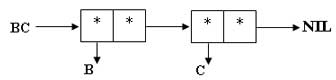
Рис.4. Определение списка BC

   $ (SETQ ABC (CONS A BC))
   (A B C)

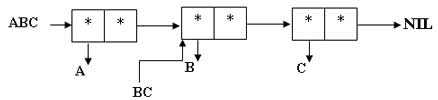
Рис.5. Определение списка ABC

   $ (SETQ SPISOK2 (CONS BC ABC))
   ((B C) A B C)

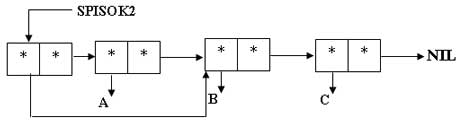
Рис.6. Определение списка SPISOK2

Таким образом, в примерах 3 и 4 мы получили два логически одинаковых списка с разной физической структурой.

Логическая структура всегда топологически имеет форму двоичного дерева, в то время как физическая структура может быть ациклическим графом (ветви могут снова сходится, но никогда не могут образовывать замкнутые циклы, т.е. указывать назад).

Замечание. В версии muLISP85 имеется еще одна интересная функция назначения: PSETQ.
Работа функции (PSETQ SYMBOL1 FORM1 ... SYMBOLN FORMN) идентична действию функции SETQ за исключением того, что все аргументы FORMj оцениваются до того, как будут сделаны любые назначения атомам SYMBOLj. Имя "PSETQ" образовано из сокращения "Parallel SETQ".

Например:

   $ (SETQ SUM 5)
   5
   $ (PSETQ SUM (+3 4) SQR (* SUM SUM))
   25
   $ SUM
   7
   $ SQR
   25

Более того, в этой версии и функция SETQ является более мощной, чем в "младших" версиях.

Функция (SETQ SYMBOL FORM) оценивает FORM, принимает за результат значение SYMBOL и возвращает результат. Отметим, что SETQ - это специальная форма и что SYMBOL не оценивается.

Если SYMBOL не является символьным атомом, то SETQ генерирует прерывание по ошибке "Несимвольный аргумент".

Если функция SETQ задана более, чем с двумя аргументами ((SETQ SYMBOL1 FORM1 SYMBOL2 FORM2 ... SYMBOLN FORMN)), то оценка форм и задание значений осуществляется последовательно. Если задано нечетное количество аргументов, то последний символ принимается за NIL. Функция SETQ возвращает новое значение последнего символа SYMBOLN. Например:

   $ (SETQ FOO '(D E F))   $ (SETQ SUM (+3 4) SQR (* SUM SUM))
   (D E F)                 49
   $ FOO                   $ SUM
   (D E F)                 7
   $ (SETQ FOO (CDR FOO))  $ SQR
   (E F)                   49
   $ FOO
   (E F)
   $ (SETQ SUM 5)
   5

Приведем макрос для этой функции:

   (DEFMACRO SETQ (SYM OBJ)
      (LIST 'SET (LIST 'QUOTE SYM) OBJ) )

На следующем шаге мы рассмотрим вопросы, связанные с управлением памятью.

Предыдущий шаг Содержание Следующий шаг