На этом шаге мы рассмотрим задачи с использованием бинарных деревьев.
Фрагмент теории
Hапомним, что:
- деревом поиска называется двоичное дерево, в котором "слева" от любой вершины находятся вершины с элементами, меньшими элемента из этой вершины, а "справа" - с большими элементами (предполагается, что все элементы дерева попарно различны и что их тип допускает применение операции сравнения);
- листом - вершина дерева, из которой не выходит ни одной ветви;
- элементом вершины называется содержимое информационного поля вершины.
"На языке LISP" бинарное дерево поиска состоит из узлов вида:
(Элемент Левое-поддерево Правое-поддерево)
В каждом узле дерева выполнено следующее условие: все элементы из узлов его левого поддерева "в некотором упорядочении" (например, по числовой величине или в алфавитном порядке) предшествуют элементу из узла и соответственно элементы из узлов правого поддерева следуют за ними.
Пример 1.
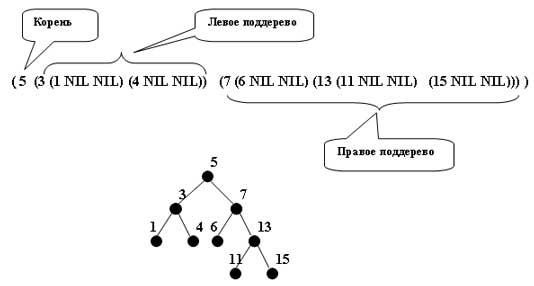
Заметим, что если TREE имеет представление вида
(Корень Левое-поддерево Правое-поддерево)
( Корень Левое-поддерево Правое-поддерево )
------ --------------- ----------------
^ ^ ^
¦ ¦ ¦
(CAR TREE) (CADR TREE) (CADDR TREE)
Пример 2. Библиотека для работы с бинарными деревьями.
(DEFUN TEST (LAMBDA NIL
(PRINT "Построим дерево со счетчиком повторяющихся элементов!")
(SETQ TREE NIL)
(LOOP
(PRINT "Введите очередной элемент дерева:")
(SETQ A (READ)) ( (EQ A '!) )
(PRINT (SETQ TREE (ADDTREE1 A TREE)))
(PRINT "---------------------------")
)
(PRINT "----------------------------------")
(PRINT "Построение дерева: ") (SETQ TREE NIL)
(LOOP
(PRINT "Введите очередной элемент дерева:")
(SETQ A (READ)) ( (EQ A '!) )
(PRINT (SETQ TREE (ADDTREE A TREE)))
)
(PRINT "-----------------------------")
(PRIN1 "Корень дерева: ")
(PRINT (ROOT TREE))
(PRIN1 "Левое поддерево: ")
(PRINT (LEFT TREE))
(PRIN1 "Правое поддерево: ")
(PRINT (RIGHT TREE))
(PRIN1 "Обход дерева в ширину: ")
(PRINT (REMBER
NIL
(LISTATOMS (UNTREE (TOP TREE) TREE))))
(PRIN1 "Левосторонний обход дерева: ")
(PRINT (UNTREE1 TREE))
(PRIN1 "Число уровней в дереве: ")
(PRINT (TOP TREE))
(PRIN1 "Количество листьев в дереве: ")
(PRINT (NLIST TREE))
(PRIN1 "Копия дерева: ")
(PRINT (TCOPY TREE))
(PRINT "-----------------------------")
(PRINT "Приступим к поиску элемента в дереве!")
(LOOP
(PRINT "Введите искомый элемент дерева:")
(SETQ A (READ))
( (EQ A '!) )
(PRINT (SEARCH A TREE))
)
(PRINT "------------------------------")
(PRINT "Приступим к удалению элемента!")
(LOOP
(PRINT "Введите удаляемый элемент дерева:")
(SETQ A (READ))
( (EQ A '!) )
(PRINT (SETQ TREE (DELETE A TREE)))
)
(PRINT "------------------------------")
(PRINT "Приступим к удалению элемента другим способом!")
(LOOP
(PRINT "Введите удаляемый элемент дерева:")
(SETQ A (READ))
( (EQ A '!) )
(PRINT (SETQ TREE (DELETE1 A TREE)))
)
(PRINT "----------------------------------")
(PRINT "Приступим к выделению поддеревьев!")
(LOOP
(PRINT "Введите какой-либо элемент дерева:")
(SETQ A (READ))
( (EQ A '!) 'END )
(PRINT (PRETREE A TREE))
(PRINT (POSTTREE A TREE))
(PRINT (UNITETREE (PRETREE A TREE)
(POSTTREE A TREE)))
(PRINT "---------------------------")
)
))
; ------------------------------
(DEFUN ADDTREE1 (LAMBDA (A TREE)
; Функция ADDTREE добавляет в дерево поиска TREE элемент A
; с подсчетом количества поторений элемента A при вводе
(COND ( (NULL TREE) (LIST (CONS A 0) NIL NIL) )
( (EQUAL A (CAAR TREE))
(LIST (CONS A (+ (CDAR TREE) 1))
(CADR TREE) (CADDR TREE)) )
( (< A (CAAR TREE))
(LIST (CAR TREE) (ADDTREE1 A (CADR TREE))
(CADDR TREE)) )
( T (LIST (CAR TREE)
(CADR TREE) (ADDTREE1 A (CADDR TREE))) )
)
))
; -----------------------------
(DEFUN ADDTREE (LAMBDA (A TREE)
; Функция ADDTREE добавляет в дерево поиска TREE элемент A
(COND ( (NULL TREE) (LIST A NIL NIL) )
( (EQUAL A (CAR TREE)) TREE )
( (< A (CAR TREE))
(LIST (CAR TREE) (ADDTREE A (CADR TREE))
(CADDR TREE)) )
( T (LIST (CAR TREE) (CADR TREE)
(ADDTREE A (CADDR TREE))) )
)
))
; -------------------------
(DEFUN CONSTR (LAMBDA (LST)
; Функция CONSTR строит дерево из списка LST в обратном порядке
(COND ( (NULL LST) NIL )
( T (ADDTREE (CAR LST) (CONSTR (CDR LST))) )
)
))
; ---------------------------
(DEFUN CONSTREE (LAMBDA (LST)
; Функция CONSTR строит дерево из списка LST в прямом порядке
(CONSTR (REVERSE LST))
))
; ----------------------------
(DEFUN SEARCH (LAMBDA (A TREE)
; Функция SEARCH ищет в дереве TREE элемент A.
; В случае успеха функция возвращает поддерево дерева
; TREE, в котором элемент A является корнем; в случае
; неудачного поиска функция возвращает NIL
(COND ( (NULL TREE) NIL )
( (EQUAL A (CAR TREE)) TREE )
( (< A (CAR TREE)) (SEARCH A (CADR TREE)) )
( T (SEARCH A (CADDR TREE)) )
)
))
; ----------------------------------
(DEFUN REPLACE (LAMBDA (OLD NEW LST)
; Замена в списке LST подсписка OLD на подсписок NEW
(COND ( (ATOM LST) LST )
( (EQUAL OLD LST) NEW )
( T (CONS (REPLACE OLD NEW (CAR LST))
(REPLACE OLD NEW (CDR LST))) )
)
))
; ------------------------
(DEFUN ROOT (LAMBDA (TREE)
; Функция ROOT возвращает корень дерева TREE
(CAR TREE)
))
; ------------------------
(DEFUN LEFT (LAMBDA (TREE)
; Функция возвращает левое поддерево дерева TREE
(CADR TREE)
))
; -------------------------
(DEFUN RIGHT (LAMBDA (TREE)
; Функция возвращает правое поддерево дерева TREE
(CADDR TREE)
))
; -----------------------------
(DEFUN RIGHTLIST (LAMBDA (TREE)
; Возвращает самый правый лист дерева TREE
(COND ( (NULL (RIGHT TREE)) (CAR TREE) )
( T (RIGHTLIST (RIGHT TREE)) )
)
))
; ----------------------------
(DEFUN LEFTLIST (LAMBDA (TREE)
; Возвращает самый левый лист дерева TREE
(COND ( (NULL (LEFT TREE)) (CAR TREE) )
( T (LEFTLIST (LEFT TREE)) )
)
))
; ------------------------------
(DEFUN DELETE (LAMBDA (ATM TREE)
; Удаление узла ATM из дерева TREE
; (нерекурсивный вариант удаления)
(SETQ SUBTREE (SEARCH ATM TREE))
(COND ( (NULL SUBTREE) (PRINT "Узла в дереве нет!") )
( T
; Узел ATM в дереве TREE найден
(COND ( (EQUAL SUBTREE (LIST ATM NIL NIL))
; Найденный узел - лист
(REPLACE SUBTREE NIL TREE)
)
( (AND (NOT (NULL (LEFT SUBTREE)))
(NOT (NULL (RIGHT SUBTREE))))
; Найденный узел имеют оба поддерева
(SETQ UZEL
(RIGHTLIST (LEFT SUBTREE)))
(RPLACA SUBTREE UZEL)
(COND ( (NULL (RIGHT
(LEFT SUBTREE)))
(REPLACE (LEFT SUBTREE)
(CADR (LEFT SUBTREE))
TREE) )
( (NULL (LEFT
(LEFT SUBTREE)))
(REPLACE (LEFT SUBTREE)
(CADDR (LEFT SUBTREE))
TREE) )
( T (REPLACE (LIST UZEL
NIL NIL)
NIL TREE) )
)
)
( (NULL (RIGHT SUBTREE))
; У найденного узла - только левое поддерево
(REPLACE SUBTREE (CADR SUBTREE)
TREE)
)
( (NULL (LEFT SUBTREE))
; У найденного узла - только правое поддерево
(REPLACE SUBTREE (CADDR SUBTREE)
TREE)
)
)
)
)
))
; -------------------------------
(DEFUN DELETE1 (LAMBDA (ATM TREE)
; Удаление узла ATM из дерева TREE
; (рекурсивный вариант удаления)
(COND ( (NULL TREE) NIL )
( (< ATM (ROOT TREE))
(LIST (CAR TREE)
(DELETE1 ATM (LEFT TREE))
(RIGHT TREE))
)
( (> ATM (ROOT TREE))
(LIST (CAR TREE)
(LEFT TREE)
(DELETE1 ATM (RIGHT TREE)))
)
( T (COND ( (NULL (RIGHT TREE)) (LEFT TREE) )
( (NULL (LEFT TREE)) (RIGHT TREE) )
( T (LIST (UD (LEFT TREE))
(DELETE1
(UD (LEFT TREE))
(LEFT TREE))
(RIGHT TREE)) )) )
)
))
; ----------------------
(DEFUN UD (LAMBDA (TREE)
; Вспомогательныя функция для функции DELETE1
(COND ( (NULL (RIGHT TREE)) (CAR TREE) )
( T (UD (RIGHT TREE)) )
)
))
; -----------------------
(DEFUN TOP (LAMBDA (TREE)
; Функция TOP возвращает число уровней в дереве TREE
; (корень дерева расположен на нулевом уровне)
(COND ( (NULL TREE) -1 )
( T (+ 1 (MAX (TOP (LEFT TREE))
(TOP (RIGHT TREE)))) )
)
))
; ----------------------
(DEFUN MAX (LAMBDA (M N)
; Функция MAX возвращает большее из чисел M и N
(COND ( (> M N) M )
( T N )
)
))
; -------------------------
(DEFUN NLIST (LAMBDA (TREE)
; Функция NLIST возвращает количество листьев дерева TREE
(COND ( (NULL TREE) 0 )
( (EQUAL (CDR TREE) (LIST NIL NIL)) 1 )
( T (+ (NLIST (LEFT TREE)) (NLIST (RIGHT TREE))) )
)
))
; -------------------------
(DEFUN TCOPY (LAMBDA (TREE)
; Функция TCOPY возвращает копию дерева TREE
(COND ( (ATOM TREE) TREE )
( T (CONS (TCOPY (CAR TREE))
(TCOPY (CDR TREE))) )
)
))
; -----------------------------
(DEFUN PRETREE (LAMBDA (A TREE)
; Функция PRETREE выделяет в отдельное дерево из дерева
; TREE все узлы, предшествующие данному элементу A
(COND ( (NULL TREE) NIL )
( (< (CAR TREE) A)
(LIST (CAR TREE) (CADR TREE)
(PRETREE A (CADDR TREE))) )
( T (PRETREE A (CADR TREE)) )
)
))
; ------------------------------
(DEFUN POSTTREE (LAMBDA (A TREE)
; Функция POSTTREE выделяет в отдельное дерево из дерева
; TREE все узлы, следующие за данным элементом A
(COND ( (NULL TREE) NIL )
( (< (CAR TREE) A)
(POSTTREE A (CADDR TREE)) )
( T (LIST (CAR TREE)
(POSTTREE A (CADR TREE))
(CADDR TREE)) )
)
))
; ------------------------------------
(DEFUN UNITETREE (LAMBDA (TREE1 TREE2)
; Функция UNITETREE объединяет два дерева поиска
; TREE1 и TREE2 в одно дерево поиска
(COND ( (NULL TREE1) TREE2 )
( (NULL TREE2) TREE1 )
( T (LIST (CAR TREE1)
(UNITETREE (PRETREE (CAR TREE1)
TREE2)
(CADR TREE1))
(UNITETREE (POSTTREE (CAR TREE1)
TREE2)
(CADDR TREE1))) ) )
))
; ----------------------------
(DEFUN UNTREE (LAMBDA (M TREE)
; "Грязный" обход дерева TREE в "ширину", начиная
; с 0-го уровня и кончая M-м уровнем
(COND ( (EQ M 0) (CAR TREE) )
( T (LIST (UNTREE (- M 1) TREE)
(SEE M TREE)) )
)
))
; ---------------------------
(DEFUN UNTREE1 (LAMBDA (TREE)
; Левосторонний обход дерева TREE
(REMBER NIL (LISTATOMS TREE))
))
; -------------------------
(DEFUN SEE (LAMBDA (N TREE)
; Обход дерева TREE в "ширину" и создание "грязного"
; списка, содержащего вершины N-го уровня дерева
(COND ( (EQ N 0) (CAR TREE) )
( (EQ N 1)
(LIST (CAR (CADR TREE)) (CAR (CADDR TREE)))
)
( T (LIST (SEE (- N 1) (CADR TREE))
(SEE (- N 1) (CADDR TREE))) )
)
))
; -----------------------------
(DEFUN LISTATOMS (LAMBDA (TREE)
; Функция LISTATOMS возвращает список, составленный из
; элементов (включая NIL !), входящих в дерево поиска TREE
(COND ( (NULL TREE) NIL)
( (ATOM (CAR TREE))
(CONS (CAR TREE) (LISTATOMS (CDR TREE))) )
( T (APPEND (LISTATOMS (CAR TREE))
(LISTATOMS (CDR TREE))) )
)
))
; -----------------------------
(DEFUN REMBER (LAMBDA (ATM LST)
; Функция REMBER возвращает список, в котором удалены
; все вхождения элемента ATM в список LST
(COND ( (NULL LST) NIL )
( (EQ ATM (CAR LST)) (REMBER ATM (CDR LST)) )
( T (CONS (CAR LST) (REMBER ATM (CDR LST))) )
)
))
; -------------------------------
(DEFUN APPEND (LAMBDA (LST1 LST2)
; Функция APPEND возвращает список, состоящий из
; элементов списка LST1, добавленных к списку LST2
(COND ( (NULL LST1) LST2 )
( (NULL LST2) LST1 )
( T (CONS (CAR LST1)
(APPEND (CDR LST1) LST2)) )
)
))
Задачи для самостоятельного решения
При работе с двоичными деревьями необходимо уметь:
- строить двоичное дерево поиска;
- осуществлять обход построенного дерева (три способа);
- находить указанную вершину в дереве;
- добавлять вершину к дереву;
- удалять вершину из дерева.
Построение
- Описать функцию (Copy T T1), которая строит дерево T1 - копию дерева T.
- Описать функцию, которая по заданному дереву T строит бинарное дерево поиска, состоящее из листьев дерева T.
- Построить бинарное дерево поиска для заданного множества целых чисел и занумеровать его вершины в соответствии с их обходом во внутреннем порядке.
- Построить бинарное дерево поиска для заданного множества целых чисел и занумеровать его вершины в соответствии с порядком прямого обхода этого дерева.
- Построить бинарное дерево поиска для заданного множества целых чисел и занумеровать его вершины в соответствии с их порядком при обратном обходе этого дерева.
- (*) В текстовом файле PROG записана (без синтаксических ошибок) программа на языке Pascal. Известно, что в этой программе каждый идентификатор (служебное слово или имя) содержит не более 9 латинских букв и(или) цифр. Напечатать в алфавитном порядке все различные идентификаторы этой программы, указав для каждого из них число его вхождений в текст программы. Для хранения идентификаторов использовать бинарное дерево поиска, элементами которого являются пары - идентификатор и число его вхождений в текст программы.
Модификация
- Написать функцию, которая добавляет к дереву T новую вершину с элементом E, если ее не было в T.
- Написать функцию, которая заменяет в дереве T значения всех отрицательных элементов вершин на их абсолютные величины (информационное поле вершины дерева содержит вещественные числа).
- Написать функцию, которая удаляет все вершины с одинаковыми элементами из непустого дерева T (использовать структуру данных множество)
- Написать функцию, которая удаляет из непустого дерева T вершины с максимальным и минимальным элементами (информационное поле вершины дерева содержит вещественные числа).
- Написать функцию, которая удаляет из непустого дерева T все вершины с положительными элементами (информационное поле вершины дерева содержит вещественные числа).
Предикаты
- Написать функцию, которая определяет, входит ли вершина, содержащая информационное поле E, в дерево T дважды.
- Написать функцию, которая проверяет, входит ли вершина, содержащая информационное поле E, в правое или левое поддерево дерева T.
- Написать функцию, которая проверяет совпадают ли элемент из самого левого листа непустого дерева T с элементом из самого правого листа того же дерева.
- Установить, можно ли попасть из одной вершины дерева в другую, если двигаться по ветвям к листьям.
- Проверить, является ли заданное дерево двоичного поиска АВЛ-деревом.
- Два дерева называется изоморфными, если можно отобразить одно из них в другое, изменив порядок сыновей его узлов. Распознать изоморфизм двух данных деревьев T1 и T2.
Подсчет
- Описать функцию, которая определяет число вхождений вершины с заданным элементом E в дерево T.
- Описать функцию, которая вычисляет сумму элементов всех вершин непустого дерева T (информационное поле вершины дерева имеет тип Real).
- Описать функцию, которая определяет максимальную глубину непустого дерева T, т.е. число ветвей в самом длинном из путей от корня дерева до листьев.
- Описать функцию, которая подсчитывает число вершин на N-ом уровне непустого дерева T (корень считать вершиной 0-го уровня).
- Написать функцию, которая определяет число вхождений элемента E в информационные поля вершин левого поддерева дерева T.
- Написать функцию, которая вычисляет среднее арифметическое всех элементов непустого дерева T (информационное поле вершины дерева содержит вещественные числа).
- Написать функцию, которая находит в непустом дереве T длину (число ветвей) пути от корня до ближайшей вершины с элементом E.
- Определить высоту дерева T, используя функцию определения пути от корня до данной вершины.
- Определить суммарный путь данного дерева Т, используя функцию определения пути от корня до данной вершины.
- Написать функцию, которая выбирает из дерева T все разные английские буквы (информационное поле вершины дерева содержит символ).
- Написать функцию, которая определяет максимальный элемент из всех листьев непустого дерева T (информационное поле вершины дерева содержит целые числа).
- Написать функцию, которая выводит содержимое информа-ционного поля всех внутренних вершин дерева.
- Выписать все вершины, находящиеся на одном уровне K, используя функцию определения пути от данной вершины до корня.
- Множество целых чисел представить в виде бинарного дерева поиска и не основе этого представления упорядочить это множество по убыванию.
На следующем шаге мы приведем задачи на использование императивного стиля программирования.
