На этом шаге мы рассмотрим гребневую регрессию и сравним ее с линейной.
Гребневая регрессия (или ридж-регрессия) также является линейной моделью регрессии, поэтому ее формула аналогична той, что используется в обычном методе наименьших квадратов. В гребневой регрессии коэффициенты (w) выбираются не только с точки зрения того, насколько хорошо они позволяют предсказывать на обучающих данных, они еще подгоняются в соответствии с дополнительным ограничением. Нам нужно, чтобы величина коэффициентов была как можно меньше. Другими словами, все элементы w должны быть близки к нулю. Это означает, что каждый признак должен иметь как можно меньшее влияние на результат (то есть каждый признак должен иметь небольшой регрессионный коэффициент) и в то же время он должен по-прежнему обладать хорошей прогнозной силой. Это ограничение является примером регуляризации (regularization). Регуляризация означает явное ограничение модели для предотвращения переобучения. Регуляризация, использующаяся в гребневой регрессии, известна как L2 регуляризация.
Гребневая регрессии реализована в классе linear_model.Ridge. Давайте посмотрим, насколько хорошо она работает на расширенном наборе данных Boston Housing:
[In 17]: from sklearn.linear_model import Ridge ridge = Ridge().fit(X_train, y_train) print("Правильность на обучающем наборе: {:.2f}".format(ridge.score(X_train, y_train))) print("Правильность на обучающем наборе: {:.2f}".format(ridge.score(X_test, y_test))) Правильность на обучающем наборе: 0.89 Правильность на тестовом наборе: 0.75
Здесь мы видим, что на обучающем наборе модель Ridge дает меньшую правильность, чем модель LinearRegression, тогда как правильность на тестовом наборе в случае применения гребневой регрессии выше. Это согласуется с нашими ожиданиями. При использовании линейной регрессии мы получили переобучение. Ridge - модель с более строгим ограничением, поэтому меньше вероятность переобучения. Менее сложная модель означает меньшую правильность на обучающем наборе, но лучшую обобщающую способность. Поскольку нас интересует только обобщающая способность, мы должны выбрать модель Ridge вместо модели LinearRegression.
Модель Ridge позволяет найти компромисс между простотой модели (получением коэффициентов, близких к нулю) и качеством ее работы на обучающем наборе. Компромисс между простотой модели и качеством работы на обучающем наборе может быть задан пользователем при помощи параметра alpha. В предыдущем примере мы использовали значение параметра по умолчанию alpha=1.0. Впрочем, нет никаких причин считать, что это даст нам оптимальный компромиссный вариант. Оптимальное значение alpha зависит от конкретного используемого набора данных. Увеличение alpha заставляет коэффициенты сжиматься до близких к нулю значений, что снижает качество работы модели на обучающем наборе, но может улучшить ее обобщающую способность. Например:
[In 18]: ridge10 = Ridge(alpha=10).fit(X_train, y_train) print("Правильность на обучающем наборе: {:.2f}".format(ridge10.score(X_train, y_train))) print("Правильность на тестовом наборе: {:.2f}".format(ridge10.score(X_test, y_test))) Правильность на обучающем наборе: 0.79 Правильность на тестовом наборе: 0.64
Уменьшая alpha, мы сжимаем коэффициенты в меньшей степени, что означает движение вправо на рисунке 1 27 шага:
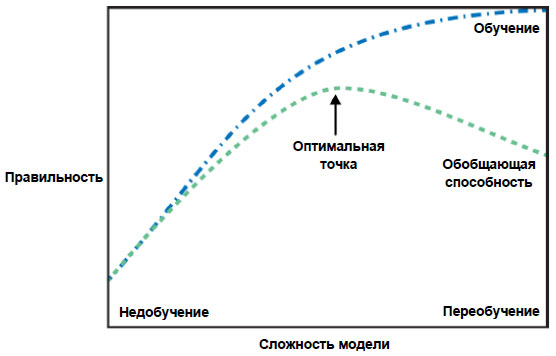
Рис.1. Рисунок 1 из 27 шага, иллюстрирующий компромисс между сложностью модели и правильностью на обучающей и тестовой выборках
При очень малых значениях alpha, ограничение на коэффициенты практически не накладывается и мы в конечном итоге получаем модель, напоминающую линейную регрессию:
[In 19]: ridge01 = Ridge(alpha=0.1).fit(X_train, y_train) print("Правильность на обучающем наборе: {:.2f}".format(ridge01.score(X_train, y_train))) print("Правильность на тестовом наборе: {:.2f}".format(ridge01.score(X_test, y_test))) Правильность на обучающем наборе: 0.93 Правильность на тестовом наборе: 0.77
Похоже, что здесь параметр alpha=0.1 сработал хорошо. Мы могли бы попробовать уменьшить alpha еще больше, чтобы улучшить обобщающую способность. Сейчас обратите внимание на то, как параметр alpha соотносится со сложностью модели (рисунок 1). Позже мы рассмотрим методы правильного подбора параметров.
Кроме того, мы можем лучше понять, как параметр alpha меняет модель, использовав атрибут coef_ с разными значениями alpha. Чем выше alpha, тем более жесткое ограничение накладывается на коэффициенты, поэтому следует ожидать меньшие значения элементов coef_ для высокого значения alpha. Это подтверждается графиком на рисунках 2, 3:
[In 20]: import matplotlib.pyplot as plt plt.plot(ridge.coef_, 's', label="Гребневая регрессия alpha=1") plt.plot(ridge10.coef_, '^', label="Гребневая регрессия alpha=10") plt.plot(ridge01.coef_, 'v', label="Гребневая регрессия alpha=0.1") plt.plot(lr.coef_, 'o', label="Линейная регрессия") plt.xlabel("Индекс коэффициента") plt.ylabel("Оценка коэффициента") plt.hlines(0, 0, len(lr.coef_)) plt.ylim(-25, 25) plt.legend()
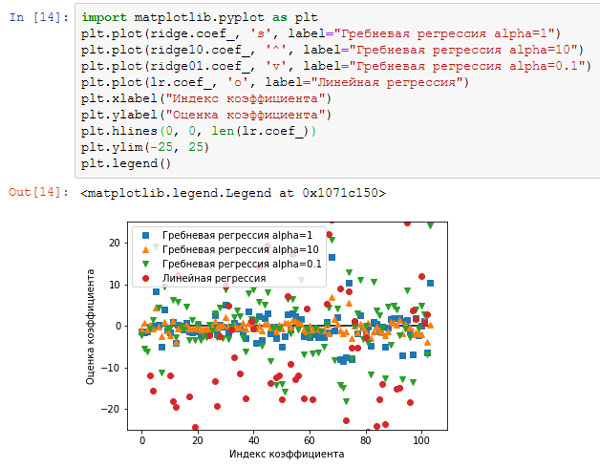
Рис.2. Сравнение оценок коэффициентов гребневой регрессии с разными значениями alpha и линейной регрессии
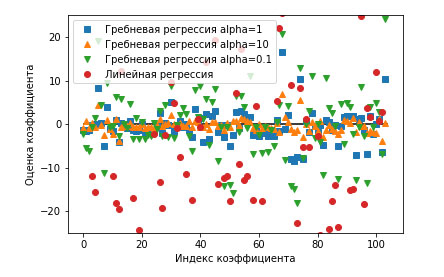
Рис.3. Отдельно график
Здесь ось х соответствует элементам атрибута coef_: x=0 показывает коэффициент, связанный с первым признаком, х=1 - коэффициент, связанный со вторым признаком и так далее, вплоть до х=100. Ось у показывает числовые значения соответствующих коэффициентов. Ключевой информацией здесь является то, что для alpha=10 коэффициенты главным образом расположены в диапазоне от -3 до 3. Коэффициенты для модели Ridge с alpha=1 несколько больше. Точки, соответствующие alpha=0.1, имеют более высокие значения, а большинство точек, соответствующих линейной регрессии без регуляризации (что соответствует alpha=0), настолько велики, что находятся за пределами диаграммы.
Еще один способ понять влияние регуляризации заключается в том, чтобы зафиксировать значение alpha и при этом менять доступный объем обучающих данных. Мы сформировали выборки разного объема на основе набора данных Boston Housing и затем построили LinearRegression и Ridge(alpha=1) на полученных подмножествах, увеличивая объем. На рисунке 4 приводятся графики, которые показывают качество работы модели в виде функции от объема набора данных, их еще называют кривыми обучения (learning curves).
[In 21]:
mglearn.plots.plot_ridge_n_samples()
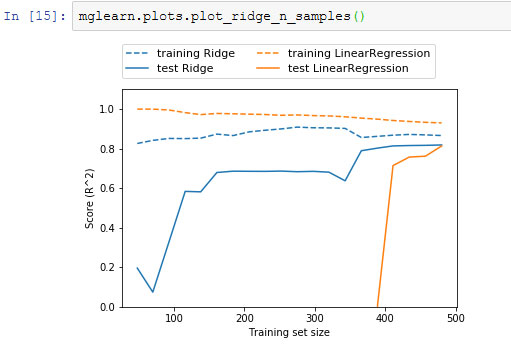
Рис.4. Кривые обучения гребневой регрессии и линейной регрессии для набора данных Boston Housing
Как и следовало ожидать, независимо от объема данных правильность на обучающем наборе всегда выше правильности на тестовом наборе, как в случае использования гребневой регрессии, так и в случае использования линейной регрессии. Поскольку гребневая регрессия - регуляризированная модель, во всех случаях на обучающем наборе правильность гребневой регрессии ниже правильности линейной регрессии. Однако правильность на тестовом наборе у гребневой регрессии выше, особенно для небольших подмножеств данных. При объеме данных менее 400 наблюдений линейная регрессия не способна обучиться чему-либо. По мере возрастания объема данных, доступного для моделирования, обе модели становятся лучше и в итоге линейная регрессия догоняет гребневую регрессию. Урок здесь состоит в том, что при достаточном объеме обучающих данных регуляризация становится менее важной и при удовлетворительном объеме данных гребневая и линейная регрессии будут демонстрировать одинаковое качество работы (тот факт, что в данном случае это происходит при использовании полного набора данных, является просто случайностью). Еще одна интересная деталь рисунка 4 - это снижение правильности линейной регрессии на обучающем наборе. С возрастанием объема данных модели становится все сложнее переобучиться или запомнить данные.
На следующем шаге мы рассмотрим лассо.
