На этом шаге мы рассмотрим использование этой функции.

В бинарной классификации возвращаемое значение decision_function имеет форму (n_samples):

[In 3]:
print("Форма массива X_test: {}".format(X_test.shape))
print("Форма решающей функции: {}".format(
    gbrt.decision_function(X_test).shape))

Форма массива X_test: (25, 2)
Форма решающей функции: (25,)

Возвращаемое значение представляет собой число с плавающей точкой для каждого примера:

[In 4]:
# выведем несколько первых элементов решающей функции
print("Решающая функция:\n{}".format(gbrt.decision_function(X_test)[:6]))

Решающая функция:
[ 4.13592603 -1.70169917 -3.95106099 -3.62609552  4.28986642  3.66166081]

Значение показывает, насколько сильно модель уверена в том, что точка данных принадлежит "положительному" классу, в данном случае, классу 1. Положительное значение указывает на предпочтение в пользу позиционного класса, а отрицательное значение - на предпочтение в пользу "отрицательного" (другого) класса.

Мы можем судить о прогнозах, лишь взглянув на знак решающей функции.

[In 5]:
print("Решающая функция с порогом отсечения:\n{}".format(
    gbrt.decision_function(X_test) > 0))
print("Прогнозы:\n{}".format(gbrt.predict(X_test)))

Решающая функция с порогом отсечения:
[ True False False False  True  True False  True  True  True False  True
  True False  True False False False  True  True  True  True  True False
 False]
Прогнозы:
['red' 'blue' 'blue' 'blue' 'red' 'red' 'blue' 'red' 'red' 'red' 'blue'
 'red' 'red' 'blue' 'red' 'blue' 'blue' 'blue' 'red' 'red' 'red' 'red'
 'red' 'blue' 'blue']

Для бинарной классификации "отрицательный" класс - это всегда первый элемент атрибута classes_, а "положительный" класс - второй элемент атрибута classes_. Таким образом, если вы хотите полностью просмотреть вывод метода predict, вам нужно воспользоваться атрибутом classes_:

[In 6]:
# переделаем булевы значения True/False в 0 и 1
greater_zero = (gbrt.decision_function(X_test) > 0).astype(int)
# используем 0 и 1 в качестве индексов атрибута classes_
pred = gbrt.classes_[greater_zero]
# pred идентичен выводу gbrt.predict
print("pred идентичен прогнозам: {}".format(
    np.all(pred == gbrt.predict(X_test))))

pred идентичен прогнозам: True

Диапазон значений decision_function может быть произвольным и зависит от данных и параметров модели:

[In 7]:
decision_function = gbrt.decision_function(X_test)
print("Решающая функция минимум: {:.2f} максимум: {:.2f}".format(
    np.min(decision_function), np.max(decision_function)))

Решающая функция минимум: -7.69 максимум: 4.29

Это произвольное масштабирование часто затрудняет интерпретацию вывода decision_function.

В следующем примере мы построим decision_function для всех точек в двумерной плоскости, используя цветовую кодировку и уже знакомую визуализацию решающей границы. Мы представим точки обучающего набора в виде кружков, а тестовые данные - в виде треугольников (рисунок 1):

[In 8]:
fig, axes = plt.subplots(1, 2, figsize=(13, 5))
mglearn.tools.plot_2d_separator(gbrt, X, ax=axes[0], alpha=.4,
                                fill=True, cm=mglearn.cm2)
scores_image = mglearn.tools.plot_2d_scores(gbrt, X, ax=axes[1],
                                            alpha=.4, cm=mglearn.ReBl)
for ax in axes:
    # размещаем на графике точки обучающего и тестового наборов
    mglearn.discrete_scatter(X_test[:, 0], X_test[:, 1], y_test,
                             markers='^', ax=ax)
    mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train,
                             markers='o', ax=ax)
    ax.set_xlabel("Характеристика 0")
    ax.set_ylabel("Характеристика 1")
    cbar = plt.colorbar(scores_image, ax=axes.tolist())
    axes[0].legend(["Тест класс 0", "Тест класс 1", "Обучение класс 0",
                    "Обучение класс 1"], ncol=4, loc=(.1, 1.1))

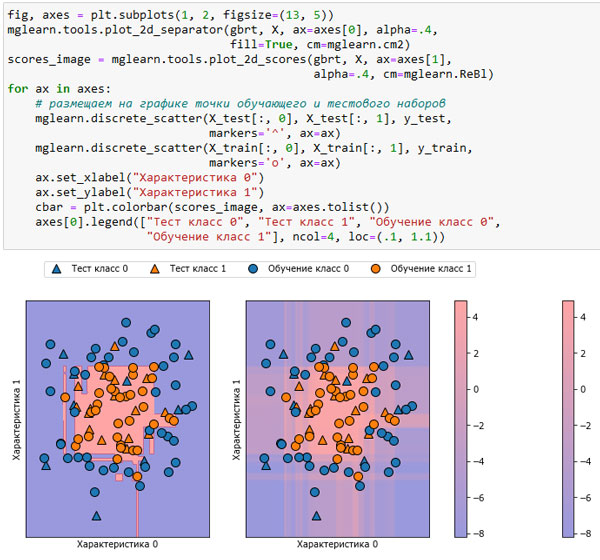
Рис.1. Граница принятия решений (слева) и решающая функция (справа) модели градиентного бустинга, построенной на двумерном синтетическом наборе данных

Цветовая кодировка не только спрогнозированного результата, но степени определенности прогноза дает дополнительную информацию.

Однако в этой визуализации трудно разглядеть границу между двумя классами.

На следующем шаге мы рассмотрим прогнозирование вероятностей.

Предыдущий шаг Содержание Следующий шаг