На этом шаге мы начнем рассматривать разработку параллельных алгоритмов умножения матрицы на вектор.
Рассмотрим операцию умножения матрицы А размерности m*n и вектора b, состоящего из n элементов. В результате операции получается вектор c размера m, каждый i-й элемент которого есть результат скалярного умножения i-й строки матрицы А (обозначим эту строчку ai) и вектора b.
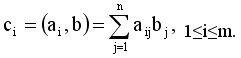
Последовательный алгоритм
Исходные данные: A[m][n] - матрица размерности m*n, b[n] - вектор, состоящий из n элементов. Результат: c[m] - вектор из m элементов.
Последовательный алгоритм умножения матрицы на вектор может быть представлен следующим образом:
for (i = 0; i < m; i++) { c[i] = 0; for (j = 0; j < n; j++) { c[i] += A[i][j]*b[j] } }
Параллельные алгоритмы
Для многих методов матричных вычислений характерным является повторение одних и тех же вычислительных действий для разных элементов матриц. Данный момент свидетельствует о наличии параллелизма по данным при выполнении матричных расчетов и, как результат, распараллеливание матричных операций сводится в большинстве случаев к разделению обрабатываемых матриц между процессорами используемой вычислительной системы. Выбор способа разделения матриц приводит к определению конкретного метода параллельных вычислений.
1. Ленточное разбиение матрицы. При ленточном разбиении каждому процессору выделяется то или иное подмножество строк (горизонтальное разбиение) или столбцов (вертикальное разбиение) матрицы. Разделение строк и столбцов на полосы в большинстве случаев происходит на непрерывной (последовательной) основе. При таком подходе для горизонтального разбиения по строкам, например, матрица A представляется в виде A = (A0, A1, …, Ap-1)T, Ai = (ai0, ai1, …, aik-1), ij = ik+ j, 0<=j<k, k = m/p, где ai = (ai1, ai2, …, ain), 0<=i<m, есть i-я строка матрицы A (предполагается, что количество строк m кратно числу процессоров p). Во всех рассматриваемых алгоритмах умножения матрицы на вектор используется разделение данных на непрерывной основе.
2. Блочное разбиение матрицы. При блочном разделении матрица делится на прямоугольные наборы элементов - при этом, как правило, используется разделение на непрерывной основе. Пусть количество процессоров составляет p = s*q, количество строк матрицы является кратным s, а количество столбцов - кратным q, то есть m=k*s и n=l*q. Представим исходную матрицу A в виде набора прямоугольных блоков следующим образом:


При таком подходе целесообразно, чтобы вычислительная система имела физическую или, по крайней мере, логическую топологию процессорной решетки из s строк и q столбцов. В этом случае при разделении данных на непрерывной основе процессоры, соседние в структуре решетки, обрабатывают смежные блоки исходной матрицы.
Анализ эффективности алгоритма умножения матрицы на вектор
Рассмотрим трудоемкость алгоритма умножения матрицы на вектор. В случае, если матрица А квадратная (m=n), последовательный алгоритм умножения матрицы на вектор имеет сложность T1=n2. В случае параллельных вычислений каждый процессор производит умножение только части (полосы) матрицы A на вектор b, размер этих полос равен n/p строк. При вычислении скалярного произведения одной строки матрицы и вектора необходимо произвести n операций умножения и (n-1) операций сложения. Следовательно, вычислительная трудоемкость параллельного алгоритма определяется выражением:
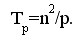
С учетом этой оценки показатели ускорения и эффективности параллельного алгоритма имеют вид:
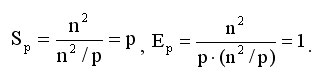
Используем предположение о том, что выполняемые операции умножения и сложения имеют одинаковую длительность 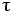 .
Кроме того, будем предполагать также, что вычислительная система является однородной, т.е. все процессоры, составляющие эту систему, обладают
одинаковой производительностью. С учетом введенных предположений время выполнения параллельного алгоритма, связанное непосредственно с вычислениями, составляет
.
Кроме того, будем предполагать также, что вычислительная система является однородной, т.е. все процессоры, составляющие эту систему, обладают
одинаковой производительностью. С учетом введенных предположений время выполнения параллельного алгоритма, связанное непосредственно с вычислениями, составляет
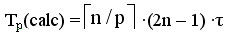
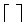 есть округление до целого в большую сторону).
есть округление до целого в большую сторону).
На следующем шаге мы закончим изучение этого вопроса.
