Этот шаг посвящен описанию и использованию функций.

    При решении задачи предыдущего шага вместо процедур удобнее было использовать функции, так как нам нужно возвратить значения из подпрограмм в основную программу (площади прямоугольника и круга). Поэтому рассмотрим основные отличия в описании и использовании функций.

    Приведем общий вид заголовка функции:

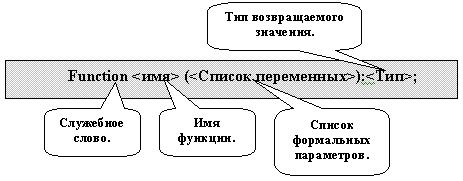
Рис.1. Общий вид заголовка функции

    Как видно из приведенной схемы существуют два отличия заголовка функции от заголовка процедуры:

• вместо служебного слова Procedure указывается служебное слово Function;
• так как функция, в отличие от процедуры, возвращает значение в основную программу, поэтому в заголовке функции указывается тип этого возвращаемого значения.

    Возврат вычисленного значения функции происходит путем выполнения в теле функции специального оператора присваивания, общий вид которого следующий (рис.2):

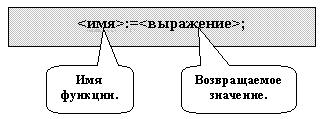
Рис.2. Общий вид специального оператора присваивания

    Приведем решение данной задачи с использованием функций.

Рис.3. Текст программы с использованием функций

    При выполнении оператора Sk:=Place_Cr(r); в функцию вычисления площади круга Place_Cr передается значение фактического параметра r, а вычисленное значение присваивается переменной Sk. Аналогичным образом осуществляется обращение к функции вычисления площади прямоугольника Place_Pr. Вычисленное значение этой функции помещается в операторе вывода Writeln.

    Таким образом, обращение к процедуре оформляется в виде отдельного оператора, а обращение к функции является частью выражения. В этом заключается отличие вызова процедуры от функции.

    В заключение дадим несколько советов, когда лучше использовать функцию, а когда процедуру:

• если подпрограмма не должна возвращать никаких значений в основную программу, то лучше использовать процедуру;
• если подпрограмма должна возвратить в основную программу одно значение, то лучше использовать функцию;
• если подпрограмма должна возвратить в основную программу более одного значения, то выбор остается за программистом.

    Прокомментируем последнее утверждение. При создании библиотек (наборов готовых подпрограмм) в настоящее время чаще всего используются функции (есть языки программирования, например, Си++, где понятие процедуры полностью отсутствует). Возвращаемое значение функции в этом случае только свидетельствует о наступлении определенного события, в то время как возврат вычисленных значений происходит через передачу параметров по ссылке.

    В качестве примера приведем текст программы для вычисления корней квадратного уравнения, которая содержит функцию нахождения корней. При решении квадратного уравнения возможно отсутствие действительных корней (когда дискриминант меньше нуля). Пусть функция возвращает значение False, когда дискриминант меньше нуля, и True - в противном случае. Если функция возвращает истинное значение, то можно брать значения параметров (там находятся корни уравнения). Если значение функции "ложь", то "забирать" значения параметров не нужно.

    Приведем текст программы:

Program Kv_Ur; 
Var
  a,b,c,x1,x2:Real;
Function Korni (k,l,m:Real; var y1,y2:Real):Boolean;
Var
  d:Real;
Begin
  d:=l*l-4*k*m; {Вычислим дискриминант.}
  If d<0 Then Korni:=False {Действительных корней нет.}
  Else
    Begin {Нахождение корней уравнения.}
       Korni:=True;
       y1:=(-l+Sqrt(d))/(2*k);
       y2:=(-l-Sqrt(d))/(2*k);
    End;
End;
Begin
  WriteLn('Задайте коэффициенты a, b, c');
  ReadLn(a,b,c);
  If Not Korni(a,b,c,x1,x2) Then WriteLn('Действительных корней нет')
  Else
    Begin 
     WriteLn('Корни уравнения');
     WriteLn('x1=',x1,' x2=',x2);
    End;
End.

    На следующем шаге мы рассмотрим области видимости имен объектов (переменных).

Предыдущий шаг Содержание Следующий шаг