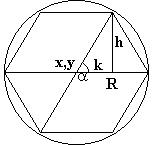
Решение опять начнем с чертежа. Для определенности возьмем шестиугольник. Существует формула, по которой можно вычислить длину стороны правильного n-угольника: a = 2Rsin(180/n) .

    Отсюда можно найти радиус описанной около многоугольника окружности:

            a
   R =  --------------
         2*sin(p/n)

    Угол при вершине a =2*p /n. Таким образом, h=R*sin(a), а k=R*cos(a).

    Используя эти формулы найдем x_sm, y_sm - смещения по осям относительно начальной точки, за которую примем точку с координатами (x+R,y). При вычислении смещений нужно учитывать, для какой точки вычисляется смещение, то есть учитывать значение счетчика i.

    Таким образом, алгоритм решения задачи может быть следующим:

• найти значение радиуса описанной окружности;
• определить координаты начальной точки;
• организовать цикл по количеству сторон многоугольника;
• вычислить смещение относительно начальной точки и сложить его с координатами начальной точки. Так получим координаты конечной точки стороны;
• построить отрезок;
• координаты конечной точки отрезка считать координатами начальной точки следующего отрезка;
• процесс повторять, пока не будут построены все стороны.

    Приведем текст программы:

Program Problem46_2;
Uses Graph;
Var
  gm,gd:Integer;
  n,a,i:Byte;
  x,y,R,x1,y1,x2,y2,x_sm,y_sm:Integer;
Begin
  Write('Количество сторон многоугольника n = ');
  ReadLn(n);
  Write('Длина стороны многоугольника a = ');
  ReadLn(a);
  WriteLn('Координаты центра описанной окружности:');
  ReadLn(x,y);
  gm:=Detect;
  InitGraph(gm,gd,'D:\BP\BGI');
  R:=Round(a/(2*sin(3.14/n))); {Радиус описанной окружности.}
  x1:=x+R; {Координаты начальной}
  y1:=y;   {точки.}
  For i:=1 To n Do
    Begin
      y_sm:=Round(R*sin(i*2*3.14/n));{Смещение относительно}
      x_sm:=Round(R*cos(i*2*3.14/n));{начальной(!) точки.  }
      x2:=x1+x_sm; {Координаты конечной}
      y2:=y1+y_sm; {точки отрезка.     }
      Line(x1,y1,x2,y2);
      x1:=x2; {Конечная точка текущего отрезка}
      y1:=y2; {становится начальной для следующего отрезка.}
    End;
  ReadLn;
  CloseGraph;
End.