На этом шаге мы перечислим возможные параметры этого аргумента.
Аргумент fmt имеет следующий формат: '[marker][line][color]'
- marker: str
- Определяет тип маркера, может принимать одно из значений, представленных в таблице 1.
| Символ | Описание |
|---|---|
| '.' | Точка (point marker) |
| ',' | Пиксель (pixel marker) |
| 'o' | Окружность (circle marker) |
| 'v' | Треугольник, направленный вниз (triangle_down marker) |
| '^' | Треугольник, направленный вверх (triangle_up marker) |
| '<' | Треугольник, направленный влево (triangle_left marker) |
| '>' | Треугольник, направленный вправо (triangle_right marker) |
| '1' | Треугольник, направленный вниз (tri_down marker) |
| '2' | Треугольник, направленный вверх (tri_up marker) |
| '3' | Треугольник, направленный влево (tri_left marker) |
| '4' | Треугольник, направленный вправо (tri_right marker) |
| 's' | Квадрат (square marker) |
| 'p' | Пятиугольник (pentagon marker) |
| '*' | Звезда (star marker) |
| 'h' | Шестиугольник (hexagon1 marker) |
| 'H' | Шестиугольник (hexagon2 marker) |
| '+' | Плюс (plus marker) |
| 'x' | Х-образный маркер (x marker) |
| 'D' | Ромб (diamond marker) |
| 'd' | Ромб (thin_diamond marker) |
| '|' | Вертикальная линия (vline marker) |
| '_' | Горизонтальная линия (hline marker) |
- line: str
- Стиль линии (таблица 2).
| Символ | Описание |
|---|---|
| '-' | Сплошная линия (solid line style) |
| '--' | Штриховая линия (dashed line style) |
| '-.' | Штрихпунктирная линия (dash-dot line style) |
| ':' | Штриховая линия (dotted line style) |
- color
- Цвет графика (таблица 3).
| Символ | Описание |
|---|---|
| 'b' | Синий |
| 'g' | Зелёный |
| 'r' | Красный |
| 'c' | Бирюзовый |
| 'm' | Фиолетовый (пурпурный) |
| 'y' | Жёлтый |
| 'k' | Чёрный |
| 'w' | Белый |
Продемонстрируем возможности plot() на примере:
import matplotlib.pyplot as plt x = [1, 5, 10, 15, 20] y1 = [1, 7, 3, 5, 11] y2 = [4, 3, 1, 8, 12] plt.figure(figsize=(12, 7)) plt.plot(x, y1, 'o-r', alpha=0.7, label='first', lw=5, mec='b', mew=2, ms=10) plt.plot(x, y2, 'v-.g', label='second', mec='r', lw=2, mew=2, ms=12) plt.legend() plt.grid(True) plt.show()
Результат работы приложения изображен на рисунке 1.
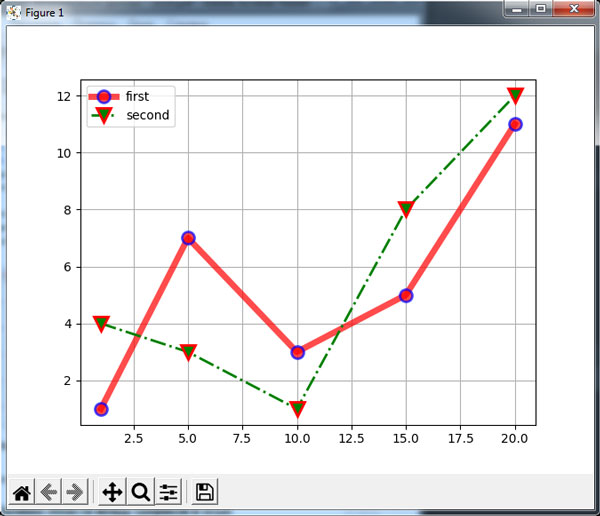
Рис.1. Графики, построенные с помощью plot()
Рассмотрим различные варианты работы с линейным графиком.
На следующем шаге мы рассмотрим заливку области между графиком и осью.
