На этом шаге мы рассмотрим особенности использования этой функции.

    Функция quiver3d() строит векторное поле по переданным координатам векторов. Библиотека предоставляет три основных варианта работы с функцией:

  quiver3d(u, v, w, ...)
  quiver3d(x, y, z, u, v, w, ...)
  quiver3d(x, y, z, f, ...)

    В первом, в quiver3d() передаются только компоненты вектора, во втором координаты и компоненты вектора, в третьем координаты и функция, которая их принимает и возвращает компоненты вектора. Компоненты и координаты - это 3D-наборы данных.

    Параметры функции quiver3d() совпадают с параметрами contour3d() с дополнительным аргументом scalars, через который можно передать массив скалярных значений.

    Подготовим набор данных и функцию, которая по координатам, возвращает компоненты вектора:

def f(x, y, z):
    return x * x, y, z


x, y, z = np.mgrid[0:3, 0:3, 0:3]
u = x * x
v = y
w = z

    Векторное поле можно построить, вызвав функцию quiver3d() с переданными компонентами и координатами...:

mlab.quiver3d(x, y, z, u, v, w, scale_factor=0.2)

mlab.show()

    (вот полный текст приложения:)

import numpy as np
from mayavi import mlab


def f(x, y, z):
    return x * x, y, z


x, y, z = np.mgrid[0:3, 0:3, 0:3]
u = x * x
v = y
w = z

mlab.quiver3d(x, y, z, u, v, w, scale_factor=0.2)

mlab.show()

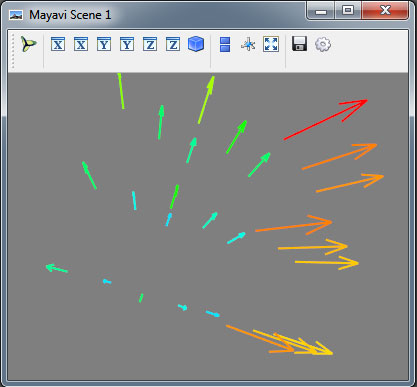
Рис.1. Демонстрация работы функции quiver3d()

    ...либо с координатами и функцией f:

import numpy as np
from mayavi import mlab


def f(x, y, z):
    return x * x, y, z


x, y, z = np.mgrid[0:3, 0:3, 0:3]
u = x * x
v = y
w = z

mlab.quiver3d(x, y, z, f, scale_factor=0.2)

mlab.show()

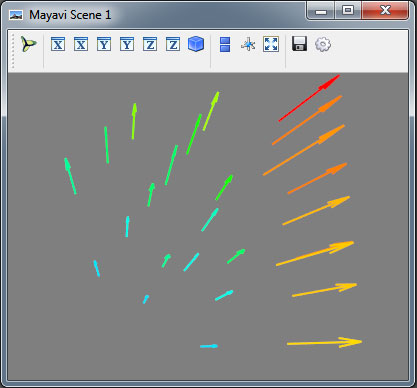
Рис.1. Демонстрация работы функции quiver3d()с использованием функции f

    В обоих случаях получим одинаковый результат.

    На следующем шаге мы рассмотрим функцию volume_slice().

Предыдущий шаг Содержание Следующий шаг