На этом шаге мы рассмотрим общие принципы использования метода опорных векторов.
Популярность метода опорных векторов (support-vector machines, SVM) сильно выросла за последние годы благодаря его высокой ошибкоустойчивости
при классификации, в том числе в пространствах высокой размерности. Как ни удивительно, SVM работает, даже если количество измерений (признаков)
превышает количество элементов данных, что необычно для алгоритмов классификации из-за так называемого проклятия размерности: при росте размерности
данные становятся очень разреженными, а это усложняет поиск закономерностей в наборе данных. Понимание основных идей SVM - необходимый шаг
становления опытного специалиста по машинному обучению.
Общее описание
Как функционируют алгоритмы классификации? На основе обучающих данных они ищут границу решений, отделяющую данные из одного класса от данных из другого. На рисунке 1 приведен пример классификатора.
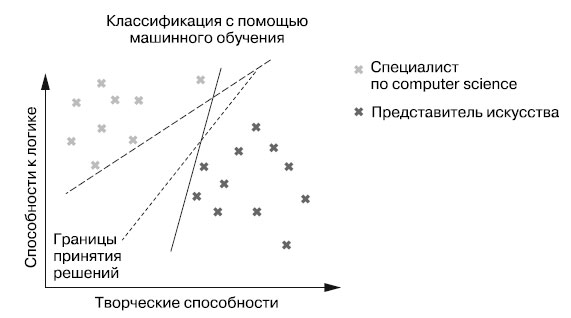
Рис.1. Различия наборов способностей специалистов по computer science и представителей искусства
Пусть нам нужно создать рекомендательную систему для студентов начальных курсов университета. На рисунке 1 визуализированы обучающие данные, состоящие из пользователей, классифицированных по их способностям в двух сферах: логика и творчество. Одни студенты отличаются сильными логическими способностями и относительно низким уровнем творческих; другие - выраженными творческими способностями и относительно низким уровнем логических. Первую группу мы обозначили как специалисты по computer science, а вторую - представители искусства.
Для классификации новых пользователей модель машинного обучения должна отыскать границу решений, разделяющую специалистов по computer science и представителей искусства. В общих чертах будем классифицировать пользователей в зависимости от того, по какую сторону границы решений они попадают. В нашем примере мы классифицируем пользователей слева от границы решений как специалистов по computer science, а справа - как представителей искусства.
В двумерном пространстве роль границы решений может играть либо прямая, либо кривая (более высокого порядка). В первом случае классификатор называется линейным (linear classifier), а во втором - нелинейным (nonlinear classifier). Далее мы будем рассматривать только линейные классификаторы.
На рисунке 1 показаны три границы решений, вполне приемлемо разделяющие данные. В нашем примере невозможно определить, какая из этих границ решений лучше; они все обеспечивают абсолютную безошибочность при классификации обучающих данных.
Но какая же граница решений лучшая?
Метод опорных векторов дает уникальный и очень красивый ответ на этот вопрос. Вполне логично, что лучшая граница решений - та, которая обеспечивает максимальный "запас прочности". Другими словами, метод опорных векторов максимизирует расстояние между границей решений и ближайшими точками данных. Цель состоит в минимизации погрешности для новых точек, близких к границе решений.
Пример этого можно увидеть на рисунке 2.
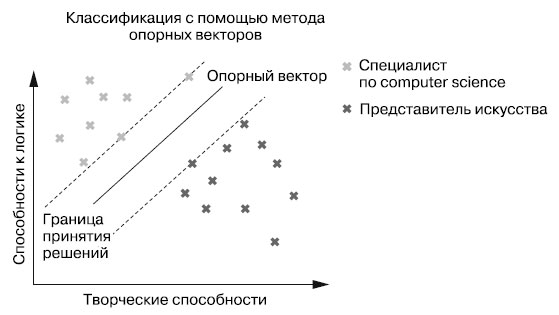
Рис.2. Метод опорных векторов максимизирует допустимую погрешность
Классификатор SVM находит такие опорные векторы, чтобы область между ними была максимально широка. В данном случае роль опорных векторов играют точки данных, лежащие на двух пунктирных линиях, параллельных границе решений. Эти прямые называются отступами (margins). Граница решений - прямая посередине, расстояние от которой до отступов максимально. Вследствие максимизации области между отступами и границей решений можно ожидать, что допустимая погрешность также будет максимальной при классификации новых точек данных.
На следующем шаге мы закончим изучение этого вопроса.
