На этом шаге мы рассмотрим важный алгоритм, используемый для вычисления расстояния Левенштейна. Разобраться в данном алгоритме сложнее, чем в предыдущих, так что заодно вы потренируете и свои навыки четкого анализа задачи.

Общее описание

Расстояние Левенштейна (Levenshtein distance) - метрика вычисления расстояния между двумя строками символов; другими словами, оно служит для количественной оценки подобия двух строк символов. Другое его название, расстояние редактирования (edit distance), в точности описывает, что именно измеряется с его помощью: сколько правок символов (вставок, удалений и замен) необходимо для преобразования одной строки в другую. Чем меньше расстояние Левенштейна, тем более схожи строки.

Расстояние Левенштейна нашло применение, в частности, в программе автоисправления в вашем смартфоне. Если вы введете в своем мессенджере Whatsapp helo, то смартфон обнаружит слово, не входящее в словарь, и выберет несколько наиболее вероятных слов для замены, после чего отсортирует их по расстоянию Левенштейна. Например, в данном случае слово с минимальным расстоянием Левенштейна, а значит максимальным подобием, - строка символов hello, так что телефон автоматически заменит helo на hello.

Рассмотрим пример с двумя менее схожими строками 'cat' и 'chello'. В таблице 1 приведена минимальная последовательность правок, необходимая для получения второй строки из первой, определяющая расстояние Левенштейна.

Таблица 1. Минимальная последовательность правок для преобразования 'cat' в 'chello'
Текущее слово Выполненная правка

cat -

cht Заменяем a на h

che Заменяем t на e

chel Вставляем l на позиции 3

chell Вставляем l на позиции 4

chello Вставляем o на позиции 5

Таблица 1. **Минимальная последовательность правок для преобразования 'cat' в 'chello'**
Текущее слово	Выполненная правка
cat	-
cht	Заменяем a на h
che	Заменяем t на e
chel	Вставляем l на позиции 3
chell	Вставляем l на позиции 4
chello	Вставляем o на позиции 5

Таблица 1 демонстрирует преобразование строки символов 'cat' в 'chello' за пять шагов, так что расстояние Левенштейна равно 5.

Код

Теперь напишем однострочник Python для вычисления расстояния Левенштейна между строками символов а и b, а и c, b и c (пример 6.4).

Пример 6.4. Вычисление расстояния Левенштейна для двух строк символов в одной строке кода

## Данные
a = "cat"
b = "chello"
c = "chess"

## Однострочник
ls = (1) lambda a, b: len(b) if not a else len(a) if not b else min(
    (2) ls(a[1:], b[1:]) + (a[0] != b[0]),
    (3) ls(a[1:], b) + 1,
    (4) ls(a, b[1:]) + 1)

## Результат
print(ls(a, b))
print(ls(a, c))
print(ls(b, c))

Архив с файлом можно взять здесь.

Попробуйте вычислить результаты работы этого фрагмента кода до запуска программы.

Принцип работы

Прежде чем углубляться в код, посмотрим на важный трюк Python, активно используемый в этом однострочнике. В Python у каждого объекта есть булево значение, равное True или False. На самом деле большинство объектов равны True, и интуитивно понятно, что можно догадаться о том, что лишь немногие объекты равны False:

числовое значение 0 равно False;
пустая строка '' равна False;
пустой список [] равен False;
пустое множество set() равно False;
пустой ассоциативный массив {} равен False.

В качестве эмпирического правила: объекты Python считаются False, если они пусты или равны нулю. Вооружившись этой информацией, мы можем взглянуть на первую часть функции для вычисления расстояния Левенштейна: создадим лямбда-функцию, принимающую на входе два строковых значения а и b и возвращающую количество правок, необходимое для преобразования а в b (1). Существуют два тривиальных случая: если строковое значение а пусто, то минимальное расстояние редактирования равно len(b), поскольку достаточно просто вставить все символы строкового значения b по одному. Аналогично, если пусто строковое значение b, то минимальное расстояние редактирования равно len(a). Это значит, если одно из этих строковых значений пусто, то можно сразу вернуть правильное расстояние редактирования.

Пусть оба строковых значения не пусты. Мы можем упростить задачу, вычислив расстояние Левенштейна меньших суффиксов исходных строковых значений а и b, как показано на рисунке 1.

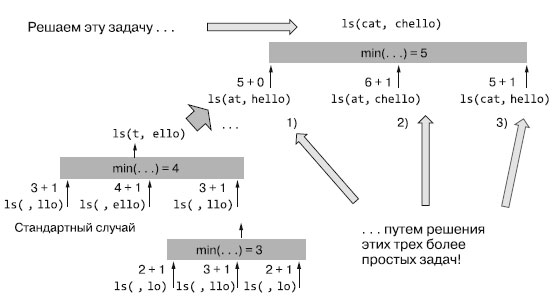
Рис.1. Рекурсивное вычисление расстояния Левенштейна для слов 'cat' и 'chello' путем вычисления сначала меньших шагов задачи

Чтобы рекурсивно вычислить расстояние Левенштейна для слов 'cat' и 'chello', сначала мы решаем более простые задачи вычисления (рекурсивно).

Вычисляем расстояние между суффиксами at и hello, поскольку если известно, как преобразовать at в hello, то можно легко преобразовать cat в chello, модифицируя сначала первый символ (или сохраняя его неизменным, если оба строковых значения начинаются с одного символа). Если это расстояние равно 5, то можно сделать вывод, что расстояние между cat и chello также не превышает 5, ведь можно получить одно из другого с помощью той же самой последовательности правок (оба слова начинаются с символа c, поэтому его редактировать не нужно).
Вычисляем расстояние между суффиксами at и chello. Если оно равно 6, то можно сделать вывод, что расстояние между cat и chello не превышает 6 + 1 = 7, поскольку можно просто убрать символ c в начале первого слова (одна дополнительная операция). А затем повторно использовать то же самое решение для получения chello из at.
Вычисляем расстояние между cat и hello. Если оно равно 5, то можно сделать вывод, что расстояние между cat и chello не превышает 5 + 1 = 6, поскольку можно просто вставить символ c в начале второго слова (одна дополнительная операция).

А поскольку это все возможные операции над первым символом (замена, удаление, вставка), то расстояние Левенштейна между cat и chello равно минимальному из трех случаев 1, 2 и 3. Теперь подробнее рассмотрим три случая в примере 6.4.

Во-первых, мы рекурсивно вычисляем расстояние редактирования между a[1:] и b[1:] (2). Если ведущие символы a[0] и b[0] различаются, то необходимо исправить ситуацию, заменив a[0] на b[0], так что мы увеличиваем расстояние редактирования на единицу. При совпадении ведущих символов решение более простой задачи ls(a[1:], b[1:]) совпадает с решением более сложной задачи ls(a, b), как вы видели на рисунке 1.

Во-вторых, мы рекурсивно вычисляем расстояние между a[1:] и b (3). Допустим, нам известен результат вычисления (преобразования a[1:] в b) - как теперь вычислить расстояние на один шаг дальше, от a до b? Ответ: просто удалить первый символ a[0] из начала a, то есть произвести ровно на одну операцию больше. Благодаря этому мы свели более сложную задачу к более простой.

В-третьих, мы рекурсивно вычисляем расстояние между a и b[1:] (4). Допустим, нам известен результат вычисления (преобразования a в b[1:]). Как теперь вычислить расстояние от a до b? В данном случае мы просто проходим на шаг больше (от a до b[1:] до b), вставляя символ b[0] в начале слова b[1:], что увеличивает расстояние на единицу.

Наконец, мы просто берем минимальное расстояние редактирования из трех (замены первого символа, удаления первого символа и вставки первого символа).

Данное однострочное решение опять демонстрирует важность навыков работы с рекурсией. Возможно, понимание рекурсии не дастся вам очень легко, но несомненно придет к вам по мере изучения множества задач на рекурсию, подобных этой.

На следующем шаге мы рассмотрим вычисление булеана с помощью функционального программирования.

Предыдущий шаг Содержание Следующий шаг