На этом шаге мы рассмотрим изоморфизм и гомеоморфизм графов.
Графы G1=(V1,E1) и G2=(V2,E2) называются изоморфными (обозначение G1~G2), если между графами существует взаимно-однозначное отображение j: G1~G2 (V1~V2, E1~E2), которое сохраняет соответствие между ребрами (дугами) графов, т.е. для любого ребра (дуги) e=(v,u) верно: e'=j(v,u)=(j(v),j(u)) (e∈E1, e'∈E2). Отображение j называется изоморфным отображением.
Иными словами, изоморфные графы различаются только обозначением вершин.
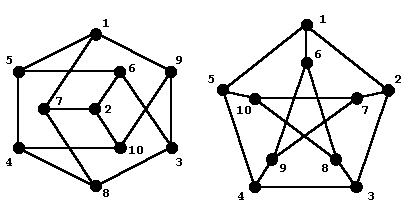
Рис.1. Изоморфные графы
Одно из изоморфных отображений: (0,0), (1,3), (2,5), (3,6), (4,7), (5,2), (6,1), (7,4), (8,9), (9,8).
Характеристики графов, инвариантные относительно изоморфизмов графов (т.е. принимающие одинаковые значения на изоморфных графах), называются инвариантами графов.
Подразделением ребра (v1,v2) графа называется операция добавления в граф вершины v' и замены этого ребра на два смежных ребра (v1,v') и (v',v2): V'=V+{v'}, E'=E-{(v1,v2)}+{(v1,v')}+{(v',v2).
Граф G' называется подразделением графа G, если он может быть получен из G путем конечного числа подразделений ребер.
На следующем шаге мы рассмотрим пути и циклы в графе.
