На этом шаге мы рассмотрим графы с атрибутами.

Во многих случаях элементам (вершинам и ребрам) графа ставятся в соответствие различные данные - атрибуты (метки). Если в качестве атрибутов используются целые или вещественные числа, то такие графы называют взвешенными. Фактически, взвешенный граф - это функция, определенная на графе. В качестве атрибутов могут выступать и нечисловые данные, поэтому я буду называть графы с атрибутами помеченными, или атрибутированными (А-графами). Например, структурные формулы химических соединений представляются молекулярными графами - А-графами, вершины которых соответствуют атомам химической структуры, а ребра - валентным связям между атомами. Для вершин молекулярного графа определен, по крайней мере, атрибут "номер атома в периодической таблице элементов", для ребер - "тип валентной связи (одинарная, двойная, тройная и др.)"; могут использоваться дополнительные атрибуты, например, заряд атома.

Для графов с атрибутами можно ввести усиленное определение изоморфизма: будем считать два А-графа изоморфными, если они изоморфны в обычном смысле, и, кроме того, изоморфное отображение сохраняет атрибуты (т.е. атрибуты соответствующих вершин и ребер в обоих графах совпадают).

Независимые множества и покрытия

Независимое множество вершин (НМВ) - множество вершин графа, никакие две вершины которого не инцидентны.

Максимальное независимое множество вершин (МНМВ) - НМВ, которое не содержится ни в каком другом НМВ.

Замечание. В данном определении "максимальность" означает "нерасширяемость"; в общем случае граф может иметь несколько МНМВ различной мощности.

Наибольшее независимое множество вершин - НМВ максимальной мощности.

Мощность наибольшего НМВ (очевидно, это одно из МНМВ) называется вершинным числом независимости графа (а также неплотностью, числом внутренней устойчивости или числом вершинной упаковки графа); обозначение - a(G).

Независимое множество ребер (НМР), или паросочетание - множество ребер графа, никакие два ребра которого не инцидентны.

Мощность наибольшего паросочетания называется числом паросочетания графа; обозначение - n(G).

Доминирующее множество вершин (ДМВ) - такое множество вершин графа, что каждая вершина графа либо принадлежит ДМВ, либо инцидентна некоторой вершине, принадлежащей ДМВ.

Вершинное покрытие (ВП) - такое множество вершин графа, что каждое ребро графа инцидентно хотя бы одной вершине, принадлежащей ДМВ.

Мощность наименьшего вершинного покрытия называется числом вершинного покрытия графа; обозначение - t(G).

Доминирующее множество ребер (ДМР), или реберное покрытие - такое множество ребер связного графа, что каждая вершина графа инцидентна хотя бы одному ребру, входящему в ДМР.

Мощность наименьшего ДМР называется числом реберного покрытия графа; обозначение - r(G).

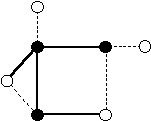
Рис.1. Пример графа

На рисунке обозначены реберное покрытии графа (пунктиром), МНМВ (белые вершины) и вершинное покрытие (черные вершины).

Величины a(G), n(G), t(G) и r(G) являются инвариантами графа. Между этими инвариантами существует связь, устанавливаемая следующими леммами.

Лемма 1.

Множество S является наименьшим вершинным покрытием графа G=(V,E) тогда и только тогда, когда T=V(G)\S является наибольшим независимым множеством вершин графа.

Доказательство.

(=>)

Докажем, что никакие две вершины, входящие в T, не инцидентны (т.е. T является НМВ). Допустим обратное: $(v_i,v_j)∈E(G), v_i∈T, v_j∈T. Но это означает, что ребро (v_i,v_j) не покрывается множеством S - противоречие с определением ВП.
T является наибольшим НМВ в силу минимальности |S| и тождества |S| + |V(G)\S| = |V(G)|.

(<=)

Докажем, что каждое ребро G инцидентно хотя бы одной вершине S (т.е. S является ВП). Допустим обратное: $(v_i,v_j)∈E(G), v_i∉S, v_j∉S. Но это значит, что v_i∉T, v_j∉T - противоречие с определением НМВ.
Аналогично доказательству (=>).

Следствие 1 леммы 1.

Для любого графа G=(V,E) сумма числа вершинного покрытия и вершинного числа независимости постоянна и равна количеству вершин G: t(G)+a(G)=|V(G)|.

Лемма 2.

Если граф G=(V,E) не имеет изолированных вершин, то сумма его числа паросочетания и числа реберного покрытия постоянна и равна количеству вершин G: n(G)+r(G)=|V(G)|.

Доказательство.

Пусть C - наименьшее реберное покрытие G, содержащее r(G) ребер. Рассмотрим подграф GC графа G, образованный множеством ребер C и инцидентными вершинами G; по определению покрытия в него входят все вершины G. Поскольку C является наименьшим, GC состоит из одной или большего количества компонент, каждая из которых является деревом (действительно, в противном случае можно было бы "выбросить" из них кольцевые ребра и получить покрытие меньшей мощности). По теореме 2 количество ребер в каждой компоненте GS_i графа GC на единицу меньше количества вершин: |E(GC_i)| = |V(GC_i)| - 1. Просуммировав эти равенства для всех i, получим: |E(GC)| = |V(GC)| - p, где p - количество компонент в GС, следовательно, p = |V(G)| - r(G). С другой стороны, если взять по одному ребру из каждой компоненты GC, получим некоторое паросочетание, следовательно, n(G) < p = |V(G)| - r(G) и n(G) + r(G) < |V(G)| (*).
Пусть M - наибольшее паросочетание G, содержащее n(G) ребер. Рассмотрим множество U вершин графа G, не покрытых М. Из определения паросочетания следует, что |U| = |V(G)| - 2*|M| = |V(G)| - 2*n(G). Множество U является независимым (действительно, если бы две произвольные вершины U "связывались" ребром, то можно было бы добавить это ребро M и получить паросочетание большей мощности). Поскольку G по условию не имеет изолированных вершин, для каждой вершины, входящей в U, существует ребро, покрывающее ее. Обозначим множество таких ребер через S. Множества M и S не пересекаются, поэтому |M ∪ S| = |M| + |S| = n(G) + |U| = |V(G)| - n(G). Объединение M и S является реберным покрытием графа по определению, следовательно, r(G) < |M ∪ S| = |V(G)| - n(G) и r(G) + n(G) < |V(G)| (**).

Из неравенств (*) и (**) следует результат леммы.

Дальнейшие результаты справедливы только для двудольных графов.

Теорема 1 (минимаксная теорема Кёнига).: Если граф G является двудольным, то t(G) = n(G) (без доказательства).
Определение.: Cовершенное паросочетание (l-фактор) - паросочетание, покрывающее все вершины графа.

Пусть X - произвольное подмножество вершин графа G=(V,E). Обозначим через G(X) множество вершин G, инцидентных вершинам X.

Теорема 2 (теорема о свадьбах).: Если G - двудольный граф с долями P₁ и P₂, то G имеет совершенное паросочетание тогда и только тогда, когда |P₁| = |P₂| и, по крайней мере, одно из P_i (i=1..2) обладает тем свойством, что для любого X ⊆ P_i выполняется неравенство |X| < |G(X)| (без доказательства).

Название теоремы связано со следующей "несерьезной" задачей: определить, возможно ли "переженить" группу юношей и девушек так, чтобы все остались довольны. Если допустить, что все "симпатии" взаимны (предположение, прямо скажем, нереалистичное), то задача сводится к нахождению совершенного паросочетания в двудольном графе, вершины одной из долей которого соответствуют юношам, другой - девушкам, и две вершины связаны ребром тогда и только тогда, когда юноша и девушка нравятся друг другу.

На следующем шаге мы рассмотрим задачу нахождения кратчайших путей.

Предыдущий шаг Содержание Следующий шаг