На этом шаге мы рассмотрим пути минимального суммарного веса во взвешенном графе, алгоритм Дейкстры, алгоритм Краскала, алгоритм Прима.
Задача: найти путь (один из путей) минимальной суммарной длины между двумя заданными вершинами взвешенного графа (орграфа) с неотрицательными весами ребер (дуг).
Классическим алгоритмом решения данной задачи является алгоритм Дейкстры. При эффективной реализации временная сложность алгоритма в худшем случае равна O(m+n log n), где m=|E|, n=|V|.
Пример прикладной задачи: необходимо добраться на самолете из города A в город B при условии, что между ними нет прямого авиационного сообщения, затратив при этом минимальные средства (при условии, что заданы возможные промежуточные аэропорты, для каждой пары аэропортов известно, существует ли между ними прямой маршрут, и если да, то известна минимальная стоимость перелета по этому маршруту).
Решение: построим взвешенный граф (орграф - если бывают "несимметричные" маршруты), вершины которого соответствуют всем возможным аэропортам, ребра (дуги) - прямым маршрутам между ними, а веса ребер (дуг) равны стоимости перелета (очевидно, неотрицательной) между соответствующими аэропортами. Задача сводится к нахождению в графе (орграфе) пути минимального веса между вершинами, соответствующими A и B.
Алгоритм Дейкстры
Дано: непyстой взвешенный гpаф G=(V,E) с неотрицательными весами ребер (дуг). Требуется найти кpатчайший пyть от s к t (s≠t).
Инициализация:
- всем веpшинам vi пpиписывается метка - вещественное число: d(s)=0, d(vi)=+- для всех vi≠s;
- метки всех вершин, кроме s, считаются временными, метка s - постоянной;
- вершина s объявляется текущей (c:=s);
- все ребра (дуги) считаются непомеченными.
Основная часть:
- для всех вершин uj, инцидентных текущей вершине c, метки которых являются временными, пересчитываем эти метки по формуле: d(uj):=min{d(uj), d(c)+Weight(c,uj)} (*), где (c,uj) - ребро (дуга), соединяющая вершины c и uj, а Weight(c,uj) - ее вес; при наличии кратных ребер выбирается ребро с минимальным весом;
- если метки всех вершин являются постоянными либо равны +-, то путь не существует; ВЫХОД("нет решения");
- иначе находим среди вершин с временными метками (среди всех таких вершин, а не только тех, чьи метки изменились в результате последнего выполнения шага (1)!) вершину x с минимальной меткой, объявляем ее метку постоянной, помечаем ребро (дугу) (c',x), такое, что d(x) = d(c')+Weight(c',x), где c'=с либо c' - вершина, бывшая текущей на одном из предыдущих шагов (c'=с, если на шаге (1) при uj=x реализовалась вторая часть формулы (*)), и делаем эту вершину текущей (c:=x);
- если c=t, то найден путь длины d(t), который можно восстановить следующим образом: это тот путь между s и t, который состоит только из помеченных на шаге (3) ребер (дуг) (можно доказать, что он существует и единственен); ВЫХОД("решение найдено");
- иначе переходим на шаг (1).
Алгоритм Дейкстры не всегда находит правильное решение в случае произвольных весов ребер (дуг) графа. Например, для орграфа, изображенного на рисунке 1, алгоритм Дейкстры найдет маршрут s(s,t)t длины 1 между вершинами s и t, а не минимальный маршрут длины 2+(-2)=0, проходящий через третью вершину графа.
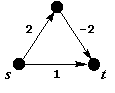
Рис.1. Пример орграфа, для которого неприменим алгоритм Дейкстры
Кратчайшее остовное дерево
Задача: найти кратчайшее остовное дерево взвешенного графа.
Пример прикладной задачи: необходимо проложить линии коммуникаций (дороги, линии связи, электропередач и т.п.) между n заданными "точечными" объектами, при условии, что, во-первых, известны "расстояния" между каждой парой объектов (это может быть геометрическое расстояние или стоимость прокладки коммуникаций между ними), и, во-вторых, объекты могут быть связаны как непосредственно, так и с участием произвольного количества промежуточных объектов.
При допущении, что разветвления возможны только в этих же n объектах, задача сводится к нахождению кратчайшего остовного дерева (SST - shortest spanning tree, или MST - minimal spanning tree) во взвешенном графе, вершины которого соответствуют заданным объектам, а веса ребер равны "расстояниям" между ними. Если каждая пара вершин соединена ребром, то граф является полным и решение существует всегда, в противном случае решение существует тогда и только тогда, когда граф связен (отсутствие ребра между двумя вершинами означает невозможность прямой связи между соответствующими объектами).
Замечание. В случае введения дополнительных точек разветвления длина кратчайшего дерева, включающего все исходные точки, а также некоторое количество новых, может быть меньше длины кратчайшего дерева, построенного только на исходных точках. Если допустить, что точки разветвления не произвольны, а берутся из некоторого множества, то задачу можно сформулировать так: построить кратчайшее дерево, покрывающее заданное подмножество вершин взвешенного графа. Данная задача, называемая задачей Штейнера, является чрезвычайно сложной с вычислительной точки зрения и может быть практически решена только при небольшом количестве дополнительных вершин. В то же время, существует эффективный приближенный алгоритм, строящий дерево, длина которого превышает длину кратчайшего дерева не более чем в два раза.
В отличие от задачи Штейнера, задача поиска кратчайшего остовного дерева допускает эффективное решение. Ниже будут рассмотрены два алгоритма решения этой задачи.
Алгоритм Краскала
Вход: связный взвешенный граф G=(V,E), n=|V|, m=|E|.
Выход: SST - кратчайшее остовное дерево G.
- SST'=<пустой граф с n вершинами>;
- k=0;
- если |E(SST')|=n-1, то SST=SST'; КОНЕЦ;
- k=k+1;
- e=<k-ое по возрастанию весов ребро графа G>;
- если добавление e в SST' не приводит к появлению цикла, то добавить его в SST';
- перейти на шаг 3.
Доказательство корректности алгоритма Краскала.
A.
Алгоритм Краскала (АК) завершает работу за конечное число шагов и строит остовное дерево графа, т.к. он является частным случаем следующего алгоритма построения остовного дерева графа (без весов).
Алгоритм построения остовного дерева графа (алгоритм ST)
Вход: связный граф G=(V,E), n=|V|, m=|E|.
Выход: ST - остовное дерево графа G.
- Занумеровать произвольным образом ребра графа G;
- ST'=<пустой граф с n вершинами>;
- k=0;
- если |E(ST')|=n-1, то ST=ST'; КОНЕЦ;
- k=k+1;
- e=<k-ое ребро графа G>;
- если добавление e в ST' не приводит к появлению цикла, то добавить его в ST';
- перейти на шаг 4.
Доказательство корректности алгоритма ST.
A.
Докажем, что алгоритм ST завершает работу не более чем за m шагов, т.е. на шаге 4 при некотором k<=m выполняется равенство |E(ST')|=n-1. Допустим обратное: |E(ST')|<n-1 при k=m (*). После выполнения шага 2 алгоритма |V(ST')|=n, следовательно, граф ST' не является связным (по следствию 1 леммы 3). Рассмотрим два произвольных связных компонента графа ST': графы T' и T''. В G не может существовать ни одного ребра, один из концов которого лежал бы в T', а другой в T'' (**) - в противном случае такое ребро было бы добавлено в ST' при некотором k<=m на шаге 7 алгоритма, т.к. это ребро заведомо не привело бы к появлению цикла. Но из (**) следует, что G несвязен - получили противоречие с (*).
B. Получаемый подграф ST является деревом по теореме 3 и является остовным деревом по определению, т.к. в него входят все вершины графа G.
- Теорема.
- АК является вариантом алгоритма ST, в котором ребра занумерованы по возрастанию весов.
- Доказательство.
- Докажем индукцией по числу ребер, что получаемое в результате работы АК остовное дерево является кратчайшим.
Базис индукции: при m=1 остовное дерево единственно, поэтому дерево, которое строит , является кратчайшим.
Допустим, что АК строит SST для всех графов G=(V,E), таких, что |E(G)|<=m. Докажем, что АК строит SST для графа G'=(V',E'): |E(G')|=m+1. Рассмотрим ребро e'∈E(G'), вес которого максимален. Возможны два варианта:
- e' - кольцевое;
- e' - ациклическое.
Рассмотрим первый случай (e' - кольцевое). Удалим e' из G'; получим связный граф G''=(V',E'\e'). В силу предположения индукции АК строит его SST. Вернемся к графу G': в силу максимальности веса e' АК "обработает" e' в последнюю очередь, поэтому при k=m граф SST'k(G') совпадает с SST(G''). При k=m+1 ребро e' не будет добавлено к SST'(G'), т.к. это привело бы к возникновению цикла, следовательно, SST(G') совпадает с SST(G''). Остается доказать, что при добавлении в связный граф ребра, вес которого не меньше, чем вес любого другого его ребра, длина кратчайшего остовного дерева графа не уменьшается. Но это верно в силу Леммы 1 (см. ниже). Таким образом, длина кратчайшего остовного дерева G' не меньше длины кратчайшего остовного дерева G''. Это минимальное значение достигается на SST(G'), следовательно, SST(G') является кратчайшим остовным деревом графа G'.
- Лемма 1.
- Пусть G=G(V,E) - связный взвешенный граф; G'=(V,E+e'), Weight(e')<=Weight(e), e"∈E(G) (*). Тогда существует кратчайшее остовное дерево графа G' , в которое не входит ребро e' (если Weight(e')>Weight(e"), e"∈E(G) (**), то e' не входит ни в какое кратчайшее остовное дерево G').
- Доказательство.
- Допустим, e' входит в кратчайшее остовное дерево T=SST(G') графа G'. Удалим из T ребро e':
T распадется на два дерева T1 и T2. Найдем в графе
G ребро e''∈E(G), один из концов которого лежит в
T1, а второй - в T2: e''=(v,u), v∈T1, u∈T2
(такое ребро существует, т.к. в противном случае G не был бы связным). Соединим деревья T1 и
T2 ребром e'': получим дерево T', которое является остовным деревом графа G', причем в силу (*)
Weight(T') = Weight(T1) + Weight(T2) + Weight(e") <= Weight(T1) + Weight(T2) + Weight(e') = Weight(T) -
построили остовное дерево не большего суммарного веса (длины), в которое не входит ребро e'; в случае (**), очевидно, Weight(T') < Weight(T).
Рассмотрим второй случай (e' - ациклическое). Удалим e' из G'; получим граф G''=(V',E'\e'), состоящий из двух связных компонент G''1 и G''2, количество ребер в каждой из которых не превосходит m. В силу предположения индукции АК построит их SST. Как и в первом случае, при k=m граф SST'k(G') совпадает с SST(G''). При k=m+1 ребро e' будет добавлено в G' на шаге 7 АК, поэтому Weight(SST'm+1(G')) = Weight(SST(G''1)) + Weight(SST(G''2)) + Weight(e'). Но это минимальное возможное значение веса кратчайшего остовного дерева G', следовательно, АК построил кратчайшее остовное дерево G'.
Алгоритм Прима
Определим расстояние между произвольной вершиной v взвешенного графа G=(V,E) и некоторым его подграфом G'⊆G как минимальный вес ребра, одним из концов которого является v, а другой лежит в G': d(v,G')=min(v,w)∈E(G), w∈G'Weight(v,w).
- SST'=<граф, состоящий из одной произвольной вершины графа G>;
- если |E(SST')|=n-1, то SST=SST'; КОНЕЦ;
- среди множества I вершин графа G, не входящих в SST', но инцидентных хотя бы одной вершине из SST' (I={u | u∈V(G), u∉SST', (u,v)∈E(G), v∈SST'}), найти вершину w∈I, расстояние которой до SST' минимально: d(w,SST')=minv∈Id(v,SST');
- добавить ребро (w,u), на котором достигается минимальное расстояние d(w,SST'), в SST';
- перейти на шаг 2.
Примем этот алгоритм без доказательства - можно доказать по аналогии с АК.
Дополнительный материал по этим вопросам можно взять здесь.
