На этом шаге мы рассмотрим теорему Радо - Эдмондса.
Хорошо известна теорема Радо-Эдмондса, которая утверждает, что если система независимости является матроидом, то для произвольной неотрицательной весовой функции градиентный алгоритм всегда находит точное решение задачи (1). Нетрудно показать, что этот результат остается верным и для случая, когда допускаются отрицательные веса.
Однако из следующей теоремы вытекает, что если система независимости отлична от матроида, то в общем случае невозможно получить оценку погрешности градиентного алгоритма.
- Теорема Радо-Эдмондса.
- Если система независимости S отлична от матроида, то для произвольных -∞ < α ≤ ∞ существует такая весовая функция c: E→R, что c(S0)=β и c(SA)=α. Причем, если β ≤ 0, то существует c: E→R_ с этим же свойством.
- Доказательство.
- Так как S отлична от матроида, то по лемме 1
∃A,B ∈ B |A| = ur(E), |B|=lr(E),
и
∃u ∈ A\B: ∀v ∈ B\A (A\u)∪v ∉ B.
Рассмотрим два случая:
- β>0. Среди всех баз, которые являются подмножествами
(A∪B)\u выберем максимальную по мощности базу C. Присвоим всем элементам
E\(A∪C) вес, условно говоря, -∞, элементам
(A∪C)\u вес
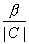, а элементу u вес 
.
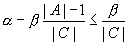Если S0 содержит u, то c(S0)=c(A)=α, иначе, очевидно,
c(S0)=c(C)=β. А т.к. a≤b, то нетрудно понять, что
c(S0) = β.
- b≤0. Среди всех баз, которые являются подмножествами (A∪B)\u, выберем базу C, для которой |C\A| минимальна. Пусть v произвольный элемент C\A. Присвоим элементам E\A∪C вес -∞, элементу u вес α, элементу v вес β, а всем остальным элементам вес 0 (в этом случае c: E → R_). Т.к. |C\A| минимальна, то любая база, веса отличного от -∞ и не содержащая u, содержит v, поэтому c(S0)=c(C)=β.
В обоих случаях можно так упорядочить элементы равного веса, что SA=A и c(SA)=α.
- β>0. Среди всех баз, которые являются подмножествами
(A∪B)\u выберем максимальную по мощности базу C. Присвоим всем элементам
E\(A∪C) вес, условно говоря, -∞, элементам
(A∪C)\u вес
Замечание. Задачу максимизации с весами c: E → R_ можно интерпретировать как задачу минимизации с весами c': E → R+ (весовой функцией c'(e)=-c(e)).
Теорема Радо-Эдмондса показывает, что для любой системы независимости, отличной от матроида, и задачи минимизации на ней (все веса неотрицательные) в принципе не может существовать гарантированной оценки погрешности градиентного алгоритма.
