Шаг 3.
Теоретическая информатика. Кодирование информации в теории Шеннона.
Понятие условной энтропии

    На этом шаге мы рассмотрим понятие условной энтропии.

    Найдем энтропию сложного опыта в том случае, если опыты не являются независимыми, т.е. если на исход оказывает влияние результат опыта . Например, если в ящике всего два разноцветных шара и состоит в извлечении первого, а – второго из них, то полностью снимает неопределенность сложного опыта   , т.е. оказывается H(  )  = H(), а не сумме энтропии, как следует из (1.5).

    Связь между на могут оказывать влияние на исходы из , т.е. некоторые пары событий A_i B_j не являются независимыми. Но тогда в (1.6)   p (A_i B_j) следует заменять не произведением вероятностей, а, согласно:

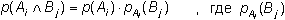
– вероятность наступления исхода B_j при условии, что в первом опыте имел место исход A_i. Тогда:

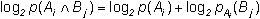
    При подстановке в (1.6) получаем:

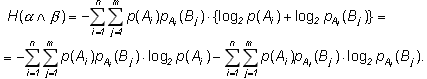
    В первом слагаемом индекс j имеется только у B; изменив порядок суммирования, получим члены вида:

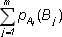
    Однако,

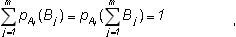
поскольку

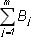
образует достоверное событие (какой-либо из исходов опыта все равно реализуется). Следовательно, первое слагаемое оказывается равным:

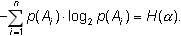
    Во втором слагаемом члены вида

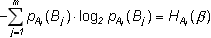(1.8)

имеют смысл энтропии опыта при условии, что в опыте реализовался исход A_i – будем называть ее условной энтропией. Если ввести данное понятие и использовать его обозначение, то второе слагаемое будет иметь вид:

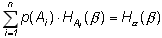(1.9)

где   есть средняя условная энтропия опыта при условии выполнении опыта . Окончательно получаем для энтропии сложного опыта:

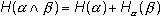(1.10)

    Полученное выражение представляет собой общее правило нахождения энтропии сложного опыта. Совершенно очевидно, что выражение (1.5) является частным случаем (1.10) при условии независимости опытов и .

    Относительно условной энтропии можно высказать следующие утверждения:

1. Условная энтропия является величиной неотрицательной. 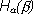 = 0 только в том случае, если любой исход полностью определяет исход 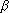(как в примере с двумя шарами), т.е.

   

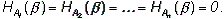
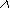
       В этом случае H (   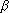 ) = H  (  ).

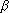2. Если опыты и независимы, то 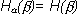, причем это оказывается наибольшим значением условной энтропии. Другими словами, опыт не может повысить неопределенность опыта 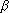; он может либо не оказать никакого влияния (если опыты независимы), либо понизить энтропию .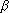

       Приведенные утверждения можно объединить одним неравенством:

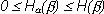   (1.11) т.е. условная энтропия не превосходит безусловную.

3. Из соотношений (1.10) и (1.11) следует, что

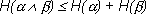   (1.12)

   причем равенство реализуется только в том случае, если опыты и 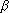независимы.

---

    Пример 1. В ящике имеются 2 белых шара и 4 черных. Из ящика извлекают последовательно два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.

    Будем считать опытом извлечение первого шара. Он имеет два исхода: A₁ – вынут белый шар; его вероятность p(A₁) = 2/6 = 1/3; исход A₂ – вынут черный шар; его вероятность p(A₂)=1 – p(A₁) = 2/3. Эти данные позволяют с помощью (1.4) сразу найти H():

H()= – p(A₁)log₂ p(A₁) – p(A₂)log₂ p(A₂) = –1/3 log₂1/3 – 2/3 log₂2/3 = 0,918 бит

    Опыт – извлечение второго шара также имеет два исхода: B₁ – вынут белый шар; B₂ – вынут черный шар, однако их вероятности будут зависеть от того, каким был исход опыта . В частности:

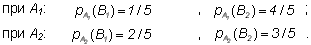
    Следовательно, энтропия, связанная со вторым опытом, является условной и, согласно (1.8) и (1.9), равна:

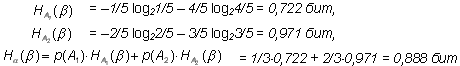
    Наконец, из (1.10): H( ) = 0,918 + 0,888 = 1,806 бит.

---

    Пример 2. Имеется три тела с одинаковыми внешними размерами, но с разными массами x₁, x₂ и x₃. Необходимо определить энтропию, связанную с нахождением наиболее тяжелого из них, если сравнивать веса тел можно только попарно.

    Последовательность действий достаточно очевидна: сравниваем вес двух любых тел, определяем из них более тяжелое, затем с ним сравниваем вес третьего тела и выбираем наибольший из них. Поскольку внешне тела неразличимы, выбор номеров тел при взвешивании будет случаен, однако общий результат от этого выбора не зависит. Пусть опыт состоит в сравнении веса двух тел, например, 1-го и 2-го. Этот опыт, очевидно, может иметь два исхода: A₁ – x₁ > x₂; его вероятность p(A₁) = 1/2; исход A₂ – x₁ < x₂; также его вероятность p(A₂)=1/2.

H() = –1/2 log₂1/2 – 1/2 log₂1/2 = 1 бит

    Опыт – сравнение весов тела, выбранного в опыте , и 3-го – имеет четыре исхода: B₁ – x₁> x₃, B₂ – x₁< x₃, B₃ – x₂> x₃, B₄ – x₂< x₃; вероятности исходов зависят от реализовавшегося исхода – для удобства представим их в виде таблицы:

B1	B2	B3	B4
1/2	1/2	0	0	A1
0	0	1/2	1/2	A2

    Вновь, воспользовавшись формулами (1.8) и (1.9), находим:

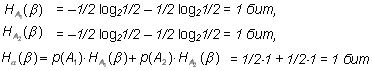
    Следовательно, энтропия сложного опыта, т.е. всей процедуры испытаний:

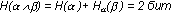
    На следующем шаге мы рассмотрим связь энтропии и информации.

Предыдущий шаг Содержание Следующий шаг