На этом шаге мы рассмотрим основные свойства примитивно рекурсивных функций.
Рекурсивные функции являются одним из вариантов уточнения понятия алгоритма. В общем, теория рекурсивных функций включает следующие классы функций:
- класс примитивной рекурсивной функции (ПРФ),
- класс общерекурсивной функции (ОРФ) и
- класс частично рекурсивной функции (ЧРФ).
В целом теория рекурсивных функций образуется следующим образом. В начале задается базис элементарных функций, затем определяются специальные операции над функциями. В результате применения определенного количества операций к элементарным функциям, строятся соответствующие классы функций: класс ПРФ, ОРФ и ЧРФ.
Примитивно рекурсивные функции (ПРФ)
Определение. Элементарными функциями называются:
- функции константы
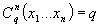, где 
;
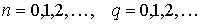- функции следования
;
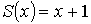- функции выбора
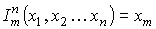, где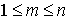 
.
Все элементарные функции - всюду определенные и алгоритмически вычислимые.
Имеется небольшое число операций над элементарными функциями, переводящими вычислимые функции снова в вычислимые.
Операция подстановки
Пусть задана функция 
и функции 
.
Определение. Говорят, что функция 
получена из этих функций с применением операции подстановки, если выполняется следующее равенство:
=
и обозначается 
, где S означает операции подстановки.
Пример 1. Пусть
и
Тогда по определению подстановки получим, что:
Пример 2. Пусть
и
Тогда по определению операции подстановки получим, что:
Как видим, это не является результатом операции подстановки, так как по условию задачи
являются трехместными функциями, а получаемая функция
f - четырехместная, что противоречит определению.
На следующем шаге мы рассмотрим основные свойства операции подстановки.
